「冬の朝、こたつが温まりきっていなくてイラッとする問題」は微分積分で解決できる(はず)。
皆さんは、微分積分というものを覚えておいででしょうか。
記憶力のある人なら「xを微分せよ」「定積分を求めよ」みたいな問題文やグラフの傾きを求めたことなどを覚えているかもしれません。しかし、それ以上に「何の役に立つのかさっぱり分からなかった」という記憶がある人の方が多いかもしれません。
そこで今回は「こんな風に役立つんだぜ」という文章問題を考えてみました。微分積分はいらない子じゃないんやで。

ライター:キグロ
5分間で数学を語るイベント「日曜数学会」や数学好きが集まる部室みたいなもの「数学デー」の主催者。数学の記事を書いたり、カクヨムで小説を書いたりしている。
問題
タカシ君はこたつでぬくぬくするのが大好き。好き過ぎて「温まりきっていないこたつ」には我慢なりません。「冬の朝、電源を入れてからしばらく待ったつもりだったけど、こたつに入ってみたらまだ寒かった」という悲劇はもう勘弁。そんな目にあうなら、布団から出たくないのです。
そこで、こたつが温まるのにかかる時間を計算することにしました。だって、あまり動かなくてもできそうだったから。

タカシ君が測定したところ、ヒーターの温度は35℃。そして、こたつの温度が10℃から30℃になるまでの時間は、ちょうど1時間でした。では、こたつを0℃から30℃まで上げるには、何時間何分何秒かかるでしょうか? ただし、こたつの温度上昇率は、こたつの温度とヒーターの温度の差に比例するものとします。
「こたつの温度が上がるのにかかる時間」を計算する方法
問題になっている状況をよく理解していないとやってしまう誤答は、たぶんこんな感じ。
- 「y=ax+b」という一次関数に当てはめると、「こたつの温度=10×時間」になりそうな気がする
- 10℃から30℃まで上げる(つまり、20度上げる)のには、1時間かかる
- では、0℃から30℃まで上げる(つまり、30度上げる)なら、1.5倍した「1時間30分」が正解になるのでは?
“こたつの温度の上がり方”に比例関係を想定した答え方ですが、これは誤り。正解は「約1時間12分32秒」です。問題文に「こたつの温度上昇率は、こたつの温度とヒーターの温度の差に比例」とあるように、この話はもっととややこしいのです。
温度上昇率が温度差に比例する……ということは、こたつの温度が上がれば上がるほど、温度上昇率は下がっていくのです。温度が上がるスピードは一定ではなく、徐々にゆっくりになっていくのです。これをグラフにすると、以下のような徐々に下がっていくグラフになります。
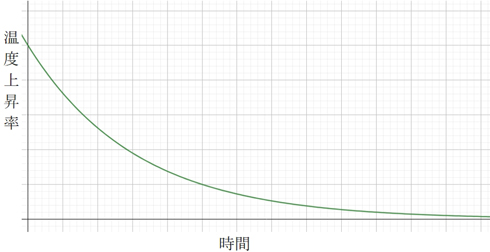
この温度上昇率は刻一刻と変化していて、1時間どころか、1秒後にはもう別の値になってしまいますから、“本当に一瞬の時間”を考える必要があります。こういうときに役立つのが微分。ものすごーく小さい間(時間でも長さでも可)に、どのくらい変化するかを表す計算です。
そして、この「小さい間の変化」を積み重ねる計算が積分です。小さい変化を0℃から30℃まで積み重ねることで、それにかかる時間を計算できます。
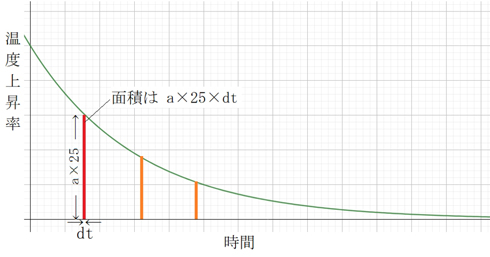
「“一瞬の時間”の温度上昇量」は、グラフの下に細い長方形の面積として現れます。でも、「瞬間」はとても短いので、例えば、1時間分、合計するにはどうすればよいのでしょうか。ここで積分の出番になります
こたつが温まるまでの時間を計算しても、タカシ君が少し快適に冬を過ごせるようになるだけでしょう。でも、「工場の炉が温まるまでの時間」は生産計画に影響しますし、「自動車のエンジンが温まるまでの時間」は車の性能や安全性に関わってきます。
そして、これらの計算にも微分と積分が使われているのです。ボルトやネジなどのように、目で見たり触ったりできるわけではないので、気付きにくいんですけどね。


