数字が1〜5しかないけど、大富豪もスピードも遊べる。
INDEX
「3」と「12」、強いのはどちらでしょうか? 変な質問ですが、「もしも大富豪だったら」と付け加えたら、誰もが「12」と答えるのではないでしょうか。
大富豪なら「(基本的に)大きな数字の方が強い」、スピードなら「場札に対して±1のカードが出せる」という風に、トランプゲームには簡単な数字の規則が用いられています。遊ぶときに意識することはほとんどありませんが、それくらい基礎的な、当たり前の知識が使われているということでしょう。
今回紹介したいのは、そんな“トランプの常識”を覆す試みをした「集合トランプ」。例えば、このトランプで遊ぶ大富豪(大“集”豪という)では{3}よりも{1,3}が強く、{1,3}よりも{1,2,3}が強く、それよりも{1,2,3,4}が強い……といった具合。このようにカードの強弱関係のような根幹的なルールをアレンジすることで、おなじみのトランプゲームの展開が大きく変わってしまうのです。

集合トランプ
スピードに集合を取り入れると、よりスピーディーなゲーム展開に
集合トランプのカードは赤/黒の2種。スペード、ハートといったスートは描かれておらず、数字は1〜5しかありません。しかし、{1,2,3}{1,2,3,4,5}と数字がいくつも書かれていたり、はたまた何も書かれていなかったり。普通のトランプは「1枚のカードで1つの数字」を表しますが、集合トランプは「1枚のカードで1つの集合」を表します。

カードは全部で32種あり、赤黒合わせて64枚。普通のトランプがジョーカー2枚を含めても54枚なので、10枚ほど多い構成
普通のトランプで遊ぶスピードは、2枚の場札に対し1つ大きい/1つ小さいカードを次々と出していく、いわば“数字の距離”を利用したゲーム。しかし、「集合スピード」では、出せるカードが「含む/含まれる」という包含関係で決まります。
直感的に理解できるので身構える必要はありません。例えば、{2,5}という場札があったとしたら、{2}{5}は出せます。{2,5}に含まれるからです。また、{2,5}を含む{2,3,5}{2,3,4,5}といったカードも出せます。しかし、{3}{3,4}{3,4,5}といったカードはダメ。{2,5}を含んでいないし、含まれてもいないからです。
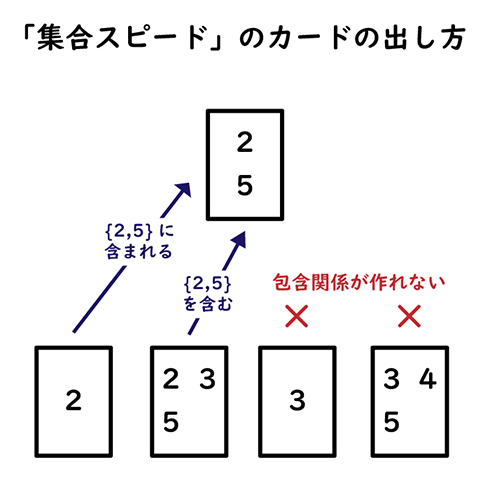
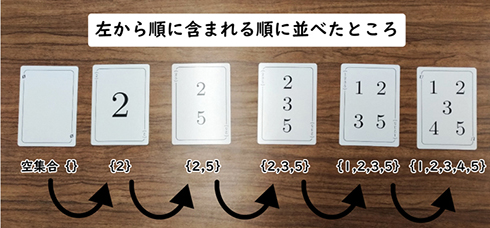
このようにゲームルールを変更すると、何が起こるでしょうか? まず、隣り合う数字(1つ大きい/1つ小さい)しか出せないという制約がなくなり、出せるカードが増えるため、ゲーム展開がよりスピーディーになります。
また、{1,2,3,4}のように集合の要素が多かったり、{1}{2}のように少なかったりした方が包含関係が作りやすいため、カードによって出しやすさが変わります。その最たる例が、全ての数字が書かれたカード{1,2,3,4,5}。全てのカードに対しても包含関係が作れるので、場札が何であっても出せますし、反対に{1,2,3,4,5}が場札のときはどんなカードでも出せます。
要するに、オールマイティーに使えるジョーカーのような存在ですね。反対に何も書かれていないカード{}も同様。どんな場札にも有効で、これが場にあるときはどんなカードでも出せます。「空集合{}は任意の集合に含まれる」という数学上のルールの応用で、「{}はあらゆるカードに含まれる」と見なされるためです。
「この“2つのジョーカー”などをうまく使って場の流れをコントロールしながら、いかに“出しにくいカード”を消化していくか」が勝敗のカギを握ることになるでしょう。
「手札を強い順に並べる」ができない集合版「大富豪」
通常のトランプで遊ぶ大富豪は「場のカードよりも強い(数字が大きい)カードを出していき、いち早く手札をなくした人が勝利」というのが基本的なルール。要するに、数字の「大きい/小さい」がカードの「強い/弱い」にそのまま反映されているわけです。
しかし、集合トランプ版の「大“集”豪」では大小関係の代わりに「含む/含まれる」という包含関係が用いられます。記事冒頭でも書いた通り、{3}よりも{1,3}が強く、{1,3}よりも{1,2,3}が強く、それよりも{1,2,3,4}が強い……といった具合。「相手を含む方が強い」という定義になっているため集合の要素数が多いほど出しやすく、全ての要素を持つ{1,2,3,4,5}が最強です。
※ちなみに、最弱は空集合{}なのですが、例外的に{1,2,3,4,5}にだけ勝てるというルール。ジョーカーとスペードの3のような関係
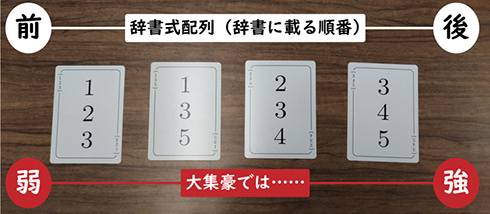
では、要素数が同じカード同士ではどうなるのか。このときは「辞書式配列(辞書で並ぶ順番)で後に来る方が強い」ということになっており、例えば、{1,2,3}より{1,3,5}、{1,3,5}より{2,3,4}、{2,3,4}より{3,4,5}が強くなります。
辞書式配列について
集合トランプでは5つの数字が使われていますが、辞書式配列は50音でも成立します。
例えば、「ねとらぼ」「とらんぷ」「ねこまた」を辞書に載る順番に並べると、「とらんぷ」「ねこまた」「ねとらぼ」の順になります。「とらんぷ」より「ねこまた」が強く、「ねこまた」より「ねとらぼ」が強いことになります。
すでに気付いている方もいるかもしれませんが、大集豪では強弱が決まらない組み合わせがたくさんあり、「“カードの相性”が悪くて出せない」とでもいうべき状況が頻発します。例えば、{1,2}と{3,4,5}は「含む/含まれる」の関係になく、要素数が違うため辞書式配列で比較することも(ルール上)できません。
このように強弱のつけ方が複雑になっているため、実際にプレイするとすぐに分かるのが「普通の大富豪では当たり前の『手札を強い順に並べて整理』が難しい」ということ。また、他のプレイヤーの手札がラスト1枚になってしまっても、強弱関係が決まらないパターンを利用して逆転できる可能性が。要素数が少ない“弱いカード”でも相手にパスさせることができ、最後まで気の抜けない展開が楽しめると思います。
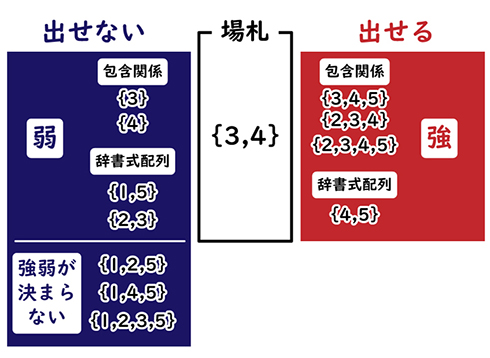
例えば、相手の最後の1枚が{1,2,3,5}でも、{3,4}を出せば上がらせないことが可能
強いカードを持っているだけでは続けられない2枚出し、3枚出し
大集豪でも、2枚出し、3枚出しは可能ですが、ちょっと複雑なルールがあります。
最初に複数枚出しをする人は全てのカードが辞書式配列で隣同士でないといけない
{1,2,3}{1,2,4}の2枚出しはできますが、{1,2,3}{1,4,5}の2枚出しはできません。3枚なら{2,4}{2,5}{3,4}などが可能です。普通の大富豪でいうところの「階段」に近い感じでしょうか。
それ以降に、複数枚出しをする場合は“カードの強弱”が重要
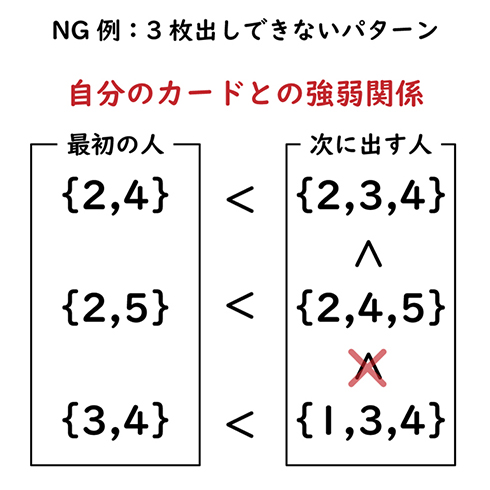
2番目以降に出す場合は、「辞書式配列で隣同士」というルールがなくなる代わりに、「相手が出したカードそれぞれに対してだけでなく、自分の出すカードそれぞれにも強弱関係を付けなければならない」というルールが課せられます。
これだけだと意味がよく分かりませんが、要は「{1,2}{3,4,5}のように強弱関係が決まらないカードはまとめて出しちゃダメ」というわけ。既述の通り、こういった組み合わせはけっこう多く、普通の大富豪よりも複数枚出しが難しくなっています。


そのため、勝負の話をするなら「弱いカードの組み合わせでもパスしてもらえる可能性が高くなっている」「4枚出す革命はかなり高難度になるため、革命返しされにくい → 革命すれば形勢逆転しやすい」といったことが言えそう。勝ち負け抜きでワイワイ遊ぶなら、複数枚出しのリレーがうまく続くだけでも場が盛り上がると思います。
集合トランプ
- 制作者:muratsuboさん(@muratsubo)
- 遊び方の詳細、その他のゲームは集合トランプのTwitterアカウント(@set_cards)、ブログからご確認ください
- BOOTHにて購入可能。価格は2400円(税込)

