【指数関数的な増え方】数学の基本から理解する“新型コロナで外出自粛などが求められる理由”（1/2 ページ）
ニュースでよく耳にする「指数関数的な増え方」、ちゃんと分かっていますか？
現在世界を震撼させている新型コロナウイルス。そのニュースで「感染者数は指数関数的に増える」と言っているのを聞いたかもしれません。
この“指数関数的な増え方”がどのようなものかご存知でしょうか？ 次の有名なクイズに答えてみてください。
【クイズで確認】“指数関数的な増え方”とは
Q：1分ごとに2倍に増える細菌がいるとします。この細菌をビーカーに1匹だけ入れたところ、1時間後にビーカーの半分まで増えました。さて、この細菌がビーカーに満杯になるには、あと何分かかるでしょうか？
答えは、1分です。なぜでしょう。
この細菌は1分で倍に増えます。ということは、ビーカーの半分を占めている状態からさらに1分たつと半分の倍に増えます。半分の倍ですから、当然満杯ですね。意外と直感的に答えるのは難しかったんじゃないでしょうか？
もうひとつ、似たクイズをやりましょう。
Q：1分ごとに数が2倍に増える細菌がいるとします。この細菌を最初、10匹用意しました。さて、10分後には何匹になっているでしょう？
シンプルな問題ですね。1分ずつ計算してみましょう。
最初10匹いた細菌は、1分後には2倍に増えて、20匹になります。2分後にはさらに2倍になって、40匹になります。3分後にはさらにさらに2倍になって、80匹です。
この調子で続けていくと、10分後には9回2倍に増えることになりますから、結局次のように計算できます。
- 10分後の数＝10×2×2×2×2×2×2×2×2×2＝5120匹
なんと、たった10匹しかいなかったのに、5000匹以上にも増えるのです！ 11分後には1万匹を超えます。
これらのクイズから分かることは「倍々に増える現象って、思ったよりも早く増えるんだな」ということです。そして、まさにこの倍々に増える現象こそが、「指数関数的に増大する現象」と呼ばれるものです。
もう少し正確に言うと、増え方が2倍である必要はなく、a倍であれば指数関数的と呼ばれます。特に、aが1より大きいと増大し、逆に1より小さいと減少します。1のときは指数関数的とは呼びません。
これを数式では、次のように書きます。
要するに、指数関数的な現象とは「現在の数が、最初の数のa倍、a倍、a倍……した数になるような現象」のことなのです。
指数関数で考える新型コロナウイルス
新型コロナウイルスの感染者も指数関数的に増えると言われます。なぜでしょうか？ それは1人から複数人に感染するためです。
1人の感染者が新たに感染させる平均の人数を「基本再生産数」と呼びます。この値が大きければ大きいほど、感染者の増え方が大きくなります。
例えば、次のようなクイズを考えてみましょう。
Q：あるウイルスの基本再生産数は2.5人です。最初10人の感染者がいたとします。この人たちから直接感染した人を2次感染者、2次感染者から感染した人を3次感染者、3次感染者から感染した人を4次感染者……と呼ぶことにします。では、10次感染者は何人になるでしょう？ また、10次感染者までの累計の感染者は、何人でしょう？
2.5という数は単なる例です。新型コロナウイルスの場合、基本再生産数はまだはっきり分かっていないようです。
さて、感染者1人から平均2.5人に感染するのですから、10人いたら10×2.5＝25人に感染します。これが2次感染者の数です。3次感染者は、これをさらに2.5倍します。すると62.5人、四捨五入して63人です。4次感染者はさらに2.5倍、5次感染者はさらにさらに2.5倍です。
結局、10次感染者までいくと、10人を9回2.5倍することになるので、このようになります。
- 10×2.5×2.5×2.5×2.5×2.5×2.5×2.5×2.5×2.5＝38147人
なんと、3万8000人を超えます！しかもこれは、10次感染者の数です。ここまでの累計では、もっと大きな数になります。
指数関数的増大の累計は、「等比数列の和の公式」というものを使って計算できます。説明は省きますが、計算してみると6万3000人超え。
最初はたった10人だったのに、9回感染するだけでこんなにも増えてしまうのです。
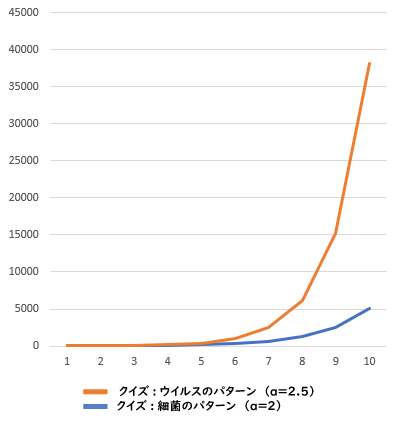
ところで、2倍ずつ増える細菌の例では、9回目で5120匹になりました。しかし1人から2.5人に感染するウイルスの例では、9回目で38147人に感染しました。2倍から2.5倍に変わっただけで、結果は7倍以上にもなってしまったのです！
これが指数関数の特徴のひとつです。aの値がちょっと増えただけで、何回かあとの結果が大きく増えるのです。逆に言うと、aの値を少し減らすだけで、あとの結果も大きく減らすことができます。
感染症対策のポイントは、まさにここにあります。
基本再生産数はウイルスの性質によって決まりますが、実際に感染する人数は人々の行動によって変えることができます。この変えたあとの値を、「実効再生産数」と呼びます。
仮に「新型コロナウイルスの基本再生産数＝3」「人々が他人との接触を減らすなどして、実効再生産数が基本再生産数から8割減した」としましょう。
このとき、実効再生産数は0.6となり、最初の感染者数が1万人だとしても10次感染者は101人にまで減ります。
現在新型コロナウイルスは世界を震撼させていますが、あれこれ考えるのは専門家たちの仕事で、われわれにできることはただひとつ。実効再生産数を少しでも減らして、感染者数を指数関数的に減少させることだけです。
これからゴールデンウィークが始まりますが、連休中もなるべく家にいましょうね。
Copyright © ITmedia, Inc. All Rights Reserved.