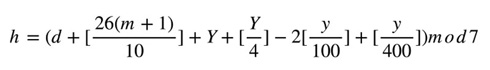「あなたの誕生日は？ ああ、その日は○曜日だね」を一瞬でできるようになる（かもしれない）方法

わかったけどわからん。

[QuizKnock，ねとらぼ]

　皆さんは、自分が生まれた日のことをどれくらい知っていますか？

　その時どんなことが流行していたかとか、その日がどんな天気だったかを親から聞かされた（あるいは調べた）、という方もいらっしゃるかもしれません。

　では、曜日は？

　今回は、「誰かの誕生日を聞いて、その曜日を当てる」ことを目標に、方法を考えてみたいと思います。

曜日を求める公式

　日付を聞いて即座に「何年何月何日？　それは●曜日だよ！」と言い当てることに憧れたことはないでしょうか。年月日も元をたどれば数字なので、計算すれば曜日を求めることが可能、というのはなんとなく想像のつくところかと思います。

　そして、この過程を公式化したものがあります。それが以下の「ツェラーの公式」と呼ばれる式です。

　西暦（グレゴリオ暦）y年m月d日の曜日を表すhは、

　なお、［x］は「xを超えない最大の整数」を、x mod nは「xをnで割った余り」を表し、式中のYは西暦の下2桁（100で割ったときのあまり）を表す。また、各年1月・2月はそれぞれ前年13月・14月として計算する。

　hが1, 2, ……, 0のとき、それぞれ日, 月, ……, 土曜日であることを表す。

　簡単にいえば、「y年m月d日」という西暦の日付から「通算の経過日数」を求め、それを7で割った余りから曜日を決定する式になっています。この式を使って計算すれば、グレゴリオ暦（現在の暦）が続く範囲ならどんな日の曜日でも求めることができます。

もう少し簡単に

　しかし、こんな長ったらしい式を覚えるのは大変！　ということで、この式をもう少しだけ簡略化して紹介しようと思います。

　「年（y）」→「月（m）」→「日（d）」の順で必要な数値を考えて足し合わせ、それを7で割って出た余りによって曜日を判定する、という方針です。

　まず、年の部分。西暦の「下2桁（上の式におけるY）」と「下2桁を4で割った商（余りは無視）」を把握します。

　ただし、1月・2月について考えたい場合はその前の年の西暦を利用します（例：2000年1月は1999年扱い）。

　次に、月に関する部分。式中の［26（m+1）/10］を毎回計算しなくても、各月のこの値を7で割った余りを覚えてしまって、その余りを式に当てはめることで正しい結果が得られます。

　例えば1と71は、「7で割った余りが1」という意味では等しいですよね。これに同じ数を足したり引いたりしても、どちらの場合でも「（7で割った）余りが同じ」ことには変わりありません（例：それぞれに10を足すと、どちらも余り4）。よって、このように簡略化することが可能といえるということです。

　ここは暗記するほかないのですが、ひとまず以下の数字の対応関係を覚えます。そして、計算する日の月と対応する数字（余り）を把握します。

　そして、日はそのまま考えます。

　今まで把握した「西暦下2桁」「下2桁を4で割った商」「月に対応する数字」「日」を足します。

　そして、1900年代生まれの場合はさらに1を足します（2000年代ならそのまま）、出てきた値を7で割ります。そして、余りと対応する曜日（日曜は1, 月曜は2……）を考えてやれば、計算終了です。

　ちなみに、「1900年代生まれの場合は〜」のところは式中の-2［y/100］+［y/400］のところを反映しています。1900年代ならこの値が-34（7で割って余り1）、2000年代なら-35（余り0）になるためです。ここで言う「●年代生まれ」にも1月・2月の前年扱いが適用される（＝2000年1月・2月は1999年扱い）ことに注意してください。

　例えば「1990年1月31日」の場合、1月なので対応する数字は1、年の下2桁は89（1月なので前年扱い）、4で割ると22（余り1）。よって89+22+1+31+1=144と計算でき、これを7で割った余りは4なので、この日は水曜日ということになります。

まとめ

　いずれの方法も覚えること自体は多いですが、計算自体に複雑な関数はほとんど使われていません。暗記さえしてしまえば、こっちのものです。

　というわけで、誕生日の曜日当てをスムーズにできるようになりたい、という方は練習あるのみだと思います。何事にも努力はつきものということで今日から特訓を始めましょう！

制作協力

QuizKnock