レベルが高過ぎて、もはや折り紙に見えない件。
INDEX
折り紙といえば、日本では比較的メジャーな遊びの1つ。「折り鶴や紙飛行機、手裏剣あたりなら、子どものころに作ったことがある」という人が、ほとんどなのではないでしょうか。
しかし、ニュースなどを見ていると、それらよりもはるかに複雑で「どうやって折っているのか全く分からない折り紙」が登場することが。ドラゴンだったり人間だったりと種類はさまざまですが、ネット上でも時々話題になっており、一度くらいは目にしたことがあるのでは?
実は、超進学校として知られる開成学園(東京都)には、ああいった“スゴい折り紙”の制作・創作を行う部活動が存在。「日本中高生折り紙連盟(JTOU)」という組織の先導的な役割を果たしているといいます。今回は、同校「折り紙研究部」を取材しました。

折り紙研究部部員が折った「龍神 3.5」(創作:神谷哲史氏)。「世界でもっとも複雑な折り紙」として知られている作品です

部長が制作した「エンシェントドラゴン」(創作:神谷哲史氏)
「複雑過ぎて、折る順番が分かる資料がない」は当たり前
取材した部員
- 大澤くん:中学3年生。折り紙研究部部長
- 金子くん:高校2年生。日本中高生折り紙連盟(JTOU)会長
- 中村くん:高校2年生。折り紙経験10年超
(学年は取材した2月下旬時点/以下、敬称略)
―― 折り紙研究部は、どういった活動をしているのですか?
大澤:開成学園は中高一貫校で、部活には中学生から高校生まで所属しています。部員数は約20人で、中学生の方がちょっと多いかな、という感じです。
活動は週2回で、展覧会、文化祭が控えている時期は作品制作がメイン。それ以外は折り紙関係の書籍を読んだり、「折り紙作家さんがこういう作品を作っていた」と雑談したり。わりと自由な感じです。
―― 素人丸出しの質問で申し訳ないんですが……あのすごーく複雑な折り紙って、どうやって折っているんですか?
大澤:折り方をステップ順に示した「折り図」が載っている本を見たことはありませんか?
制作するときは、それを作家さんごとにまとめた書籍を見たり、日本折紙学会が隔月で刊行している雑誌「折紙探偵団マガジン」を参考にしたりしています。
―― それだけ聞くと、わりと普通の折り紙に近い印象を受けますね。
大澤:ただ、必ずしも折り図が用意されているわけではなくて、そういうときは「展開図」を見て作ることになります。折るのに必要な線だけが描かれたもので、山折り/谷折りは線の色で分かりますが、手順などは記載されていません。
―― 「開いた折り紙から、元の作品を復元する」のとあまり変わらない気がするんですが……。大変ではないんですか?
中村:折り図って、作るのが大変なんですよ。完成までに必要な工程の数だけ図を用意すると、場合によっては数百枚になってしまいますし。「自分じゃなくて、他人のために作るもの」ですね。
金子:折り図を作ってくれる人は……マジで良心的だと思います。
大澤:その点、展開図はオリジナル作品を考えるときに使われることが多いので、わざわざ用意する必要がないんです。例えば、僕の創作作品の展開図はこんな感じで、折ると「掛け時計」になります。
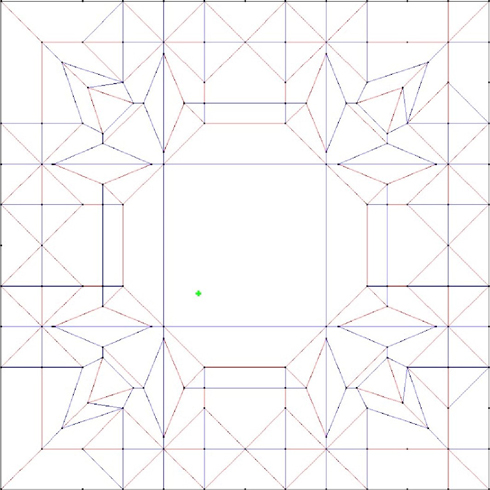
大澤くん創作「掛け時計」の展開図。これを折ると……

ローマ数字が刻まれた四角い時計に
―― 赤、青色の線が規則的に配置されていて、幾何学模様みたいな美しさがありますね。どうやって折ったらいいかは、さっぱり分かりませんが……。
大澤:折り紙をしている人全体で考えると、だいたいの人が「折り図があれば作れる」段階で止まっていて、その先に「展開図から考えて折れる人」。さらに進むと、他人の作品を折る“制作”だけでなく、自分の作品を作る“創作”もしている人たちがちょっといる感じ。うちの部活でも、全員が創作までやっているわけではありませんね。
折り紙創作のテクニック:円分子法
―― 折り紙といえば「折り鶴、手裏剣などの既存作品を作る」のが一般的な楽しみ方。創作は、どうすればできるようになるんですか?
中村:……“角(かど)を出す”ことを意識すればいいんじゃないかなあ。「出したい角をどうやって紙に配置するか」というか。
―― 角を出す……?


