実際のところ“インド式計算法”って便利なんです？ 本場インド人が解説したら、爆速過ぎて会場がザワザワした話（1/2 ページ）
計算方法が違い過ぎて、魔法か何かに見えてしまう。
「難しい問題もあっという間に解けるようになる」といわれている、いわゆる“インド式計算法”。日本ではあまり使われていませんが、どれほど便利なものなのでしょうか。
今回取り上げるのは、数学イベント「マスパーティ」内で行われた、インド出身のプサパティ シバラムさんによる“インド式計算法”の発表。日本の学校で教わるものとは全く違う魔法のような解き方に、客席は何度もざわめいていました。
本記事は下記イベントでの発表「ウェーダ式数学」の書き起こしとなります
- イベント：2019年10月19、20日開催「マスパーティ」（Twitter：@mathparty2019）
- 発表者：プサパティ シバラムさん（Facebook：vedicmathsjapan）
タイトルに「数学を学ぶ自然の道」と書いています。人生においても数学においても解決する道はたくさんあると思うんですが、「自然の道」は1つだけなんじゃないかと。
自然の道とはどういうものかというと、まず「努力が少ないが、効果は素晴らしい」。英語では「effortless」といいます。それから「直感的」で、一目見て「あ、これは最適だな」と思えるような道（方法）。そして「魔法でもあり、手法でもある」。
数学における自然の道は、ウェーダ式数学（いわゆるインド式数学）と言いたいところ。今日はその掛け算と割り算、時間があればスクエア（平方数）とルートの求め方を紹介したいと思います。
掛け算のやり方
掛け算は縦方向、斜め方向の計算で解きます。例えば「31×32」なら、3つのステップで1桁ずつ答えを出していきます。
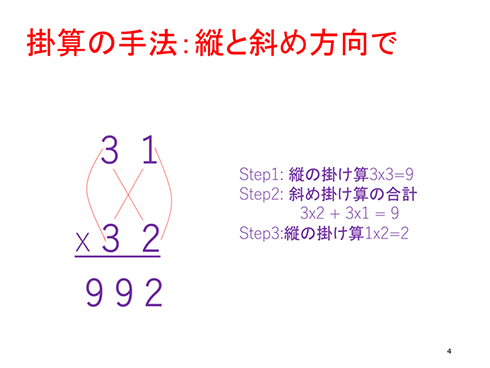
31×32の解き方
- STEP1：縦の掛け算（10の位同士）：3×3＝9
- STEP2：斜めの掛け算（10の位、1の位）の合計：「3×2」「3×1」を足して9
- STEP3：縦の掛け算（1の位同士）：1×2＝2
これで終わりです。各ステップで出た数字を並べた「992」が答えですね。
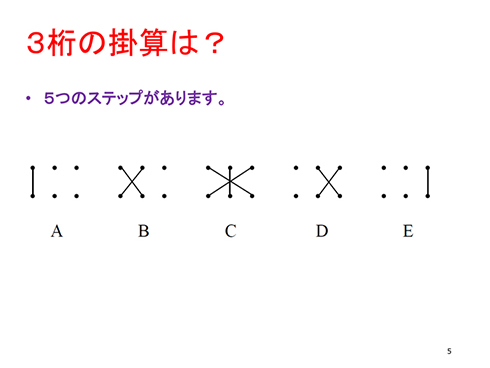
3桁の場合はステップが5つに増えますが、何桁×何桁でも同じように計算できます。
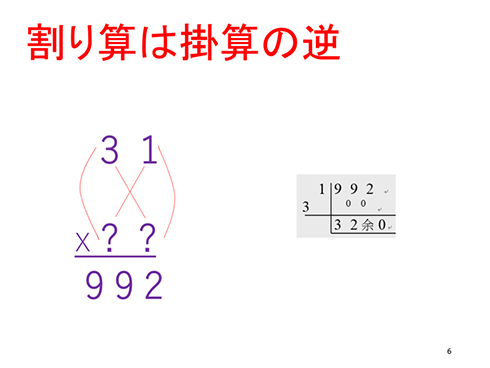
割り算のやり方
割り算は掛け算の逆をやればよくて、「割る・掛ける・引く」を繰り返せば何でも解けます。
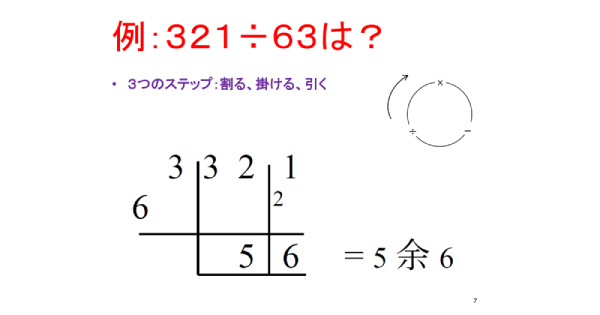
例えば、「321÷63」。最初の1桁（63の6）だけを割り算に使います。残りの桁は「旗を立てる」というんですが、「3」を持ち上げて書いてますよね。
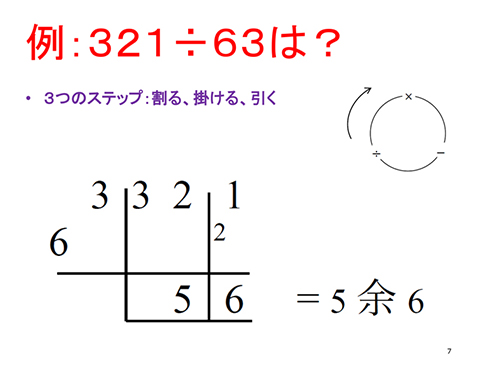
321÷63の解き方
- STEP1：割るステップ。32を6で割る（5余り2）
- STEP2：掛けるステップ。先ほどの5と、旗に立てた3で掛け算（15）
- STEP3：引くステップ。STEP1の余り2、321の1を組み合わせた21から、STEP2の15を引く（6）
というわけで、答えは「5余り6」。これだけです。
会場：どよめき＆笑い（日本の学校で教わる計算方法と違いすぎて、合っているのが不思議だったもよう。以下、頻繁に起こるので省略）
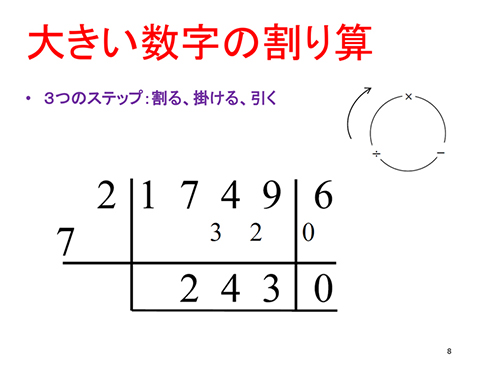
17496÷72のような大きな数字の割り算でもやり方は同じです。割る、掛ける、引くの繰り返し。小学1〜2年生にも普通に教えるんですよ、これ。
この計算方法は代数でも使えるんですね。「1/1＋x」の場合、「1＋x」の1とxのどちらを割る数、旗に立てる数にするかで、異なるTaylor series（テイラー級数）の拡張が出せます。
※テイラー級数：関数のある一点での導関数たちの値から計算される項の無限和として関数を表したものである。そのような級数を得ることをテイラー展開という（Wikipediaより）。
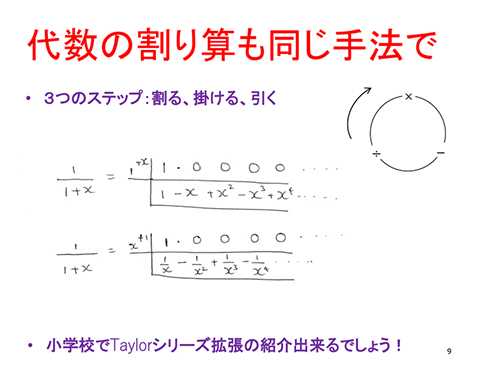
小学校で普通に教えられるものなんですよ、これ。
Copyright © ITmedia, Inc. All Rights Reserved.