ゼータ愛。
数学との関わり方は人それぞれ。学校で教わってそれきりになってしまう人もいれば、仕事などで使っている人も。そして、数学の世界に魅力を感じ、自分なりの仕方で楽しみ続けている人もいます。
今回紹介するのは、2019年10月に「数学の楽しみ方の見本市」と銘打って開催された数学イベント「マスパーティ」内のある発表。ゼータ関数を学ぶだけでは飽きたらず、食べたり、触ったり……と斜め上の楽しみ方をしているという、辻順平さんによるもの。
アクティブ(?)過ぎる数学愛が目を引きますが、数式を使わずにゼータ関数のアレコレについて解説しており、「リーマンの素数公式って何?」という方も楽しめそうです。
本記事は下記イベントでの発表「ゼータ関数の楽しみ方」の書き起こしとなります
- イベント:2019年10月19、20日開催「マスパーティ」(Twitter:@mathparty2019)
- 発表者:辻順平さん(Twitter:@tsujimotter/ブログ:tsujimotterのノートブック)
「素数階段」が再現できるゼータ関数

今日は「ゼータ関数の楽しみ方」というタイトルで発表させていただきます。私はゼータ関数が大好きなんですけど、その楽しんでいる様子を紹介したいなあと思っております。
私がゼータ関数に興味を持ったきっかけになったのは「素数の音楽」(著マーカス・デュ・ソートイ/イギリスの数学者)という本と、「リーマン予想 天才たちの150年の闘い」というNHKの番組です。

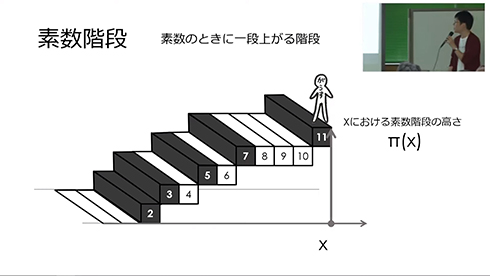
同番組には、ドイツの天才数学者・ガウスが、天に向かって延びる「素数階段」を登っていく謎のCG映像が出てくるんですけど。その階段は素数のところで1段上がり、xまで行ったときにx以下の素数の個数が分かるようになっています。
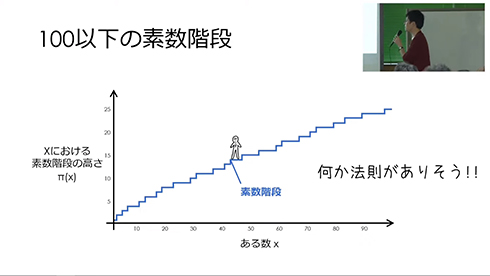
100以下の素数階段はこんな感じで、何か法則がありそうな形をしているんですよね。漠然と「何かありそう」というだけだとアレなんですが、ここにバチッとハマる法則が見つかったら面白いなあ、と思うわけです。
ここに対して、最初の重要なアプローチをしたのが、今回テーマであるゼータ関数なんです。


ゼータ関数をプロットするとこんな感じになります。へこんでいるところが「零点」です。

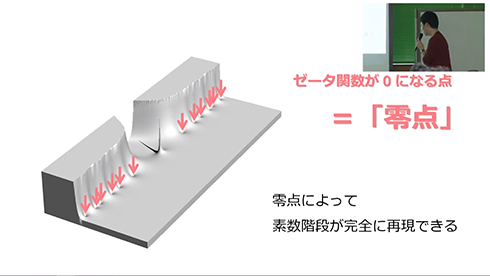
この零点を原点に近いところからピックアップして、とある変換を行います。すると、第1の零点ではこんな感じの波、第2の零点ではこんな感じの波が作れます。
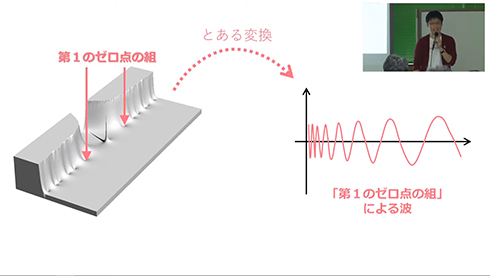
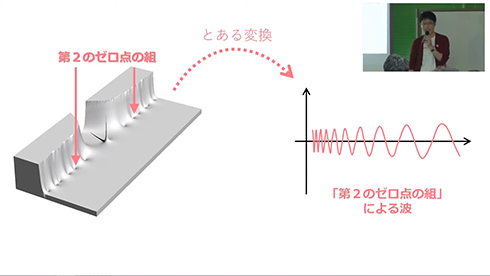
これは一体何なのか。もともと対数積分という素数階段に似た曲線があるんですが、そこに先ほどの“零点の波”を足し合わせると、素数階段が完全に再現できる、というのがスゴいことなんです。
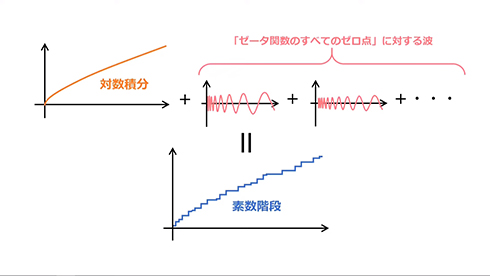
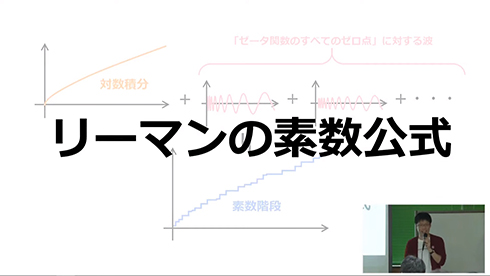
これが「リーマンの素数公式」と呼ばれるもので、素数の世界とゼータ関数の世界をつなぐ架け橋になっているんですね。私の大好きな公式の1つです。……大好き(大事なことなので2回言ったもよう)なんですけど、好き過ぎて仕方がないので、どうにかして理解したいなと思ってこんなものを作ってみました。
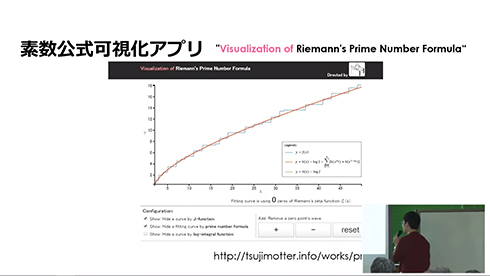
「先ほどの対数積分に対して“波”を加えていくと、どのような曲線ができるのか」をグラフ化したものです。最初の1個を足すと、曲線がうにょっと動きます。2個、3個、4個……と組み合わせていくと、どんどん素数階段に近い形になっていって、30個くらい足してしまうとほぼ階段と同じような形になります。
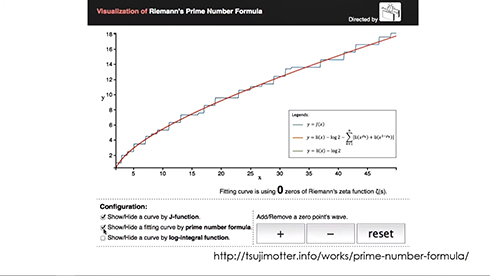
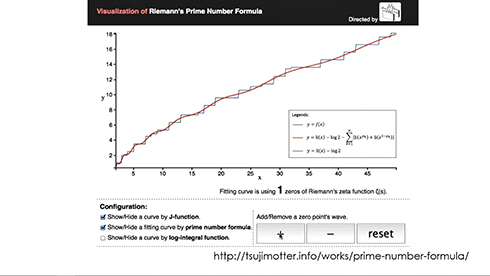
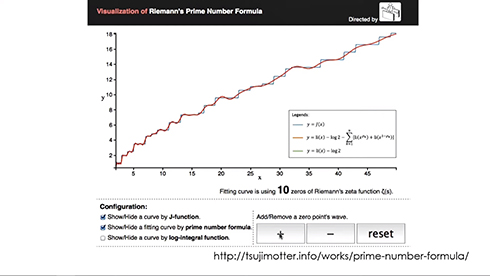
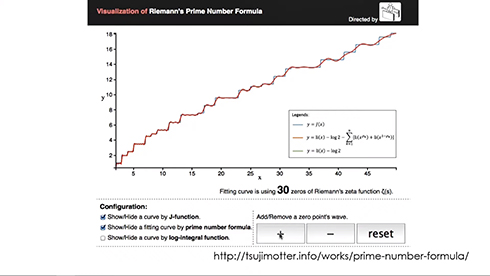
図ではよく見たんですがアニメーションするものがなかったので、計算して自分で描いたということに自分の喜びがありました。
触れるゼータ関数

愛着がわくと、もっと身近に感じたくなるわけですよね。
で、「触りたい!」と思って、Rubyのプログラムを使って、ゼータ関数の数式の3Dデータを作りまして、3Dプリンタで「触れるゼータ関数」を作りました。
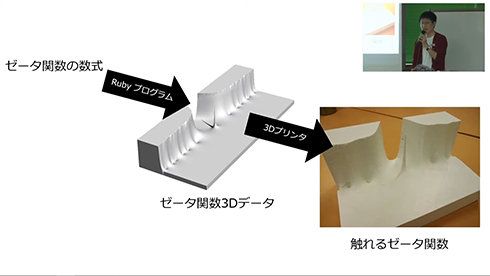
この「触れるゼータ関数」は「DMM.make」というサイトで2種類販売しています。お求めやすいミニエディションは4447円、フルエディションは29万8999円。価格はどちらも素数となっています。
※なお、この金額は「消費税8%の税込価格」。消費税が10%に上がったことで、素数ではなくなってしまったとのこと。まさか増税の影響が、ゼータ関数にも降りかかるとは……


こんなモン誰が買うんだって思うかもしれませんが、5人くらい買っています。やっぱり“ゼータ愛”って伝わるんだな、って思いました。
会場:笑い


