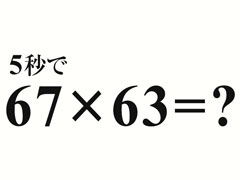「67×63」を一瞬で解けるようになる方法

インド人に学ぶヴェーダ数学。

[QuizKnock，ねとらぼ]

　突然ですが、問題です。67×63は？　制限時間は5秒です。

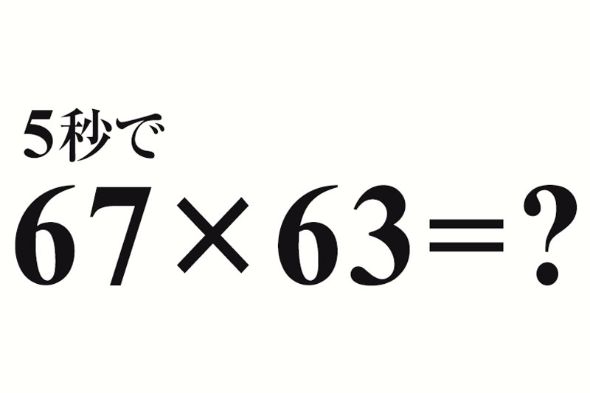
　どうですか、5秒で解けましたか？

　解けたアナタは素晴らしい。おめでとうございます。

　解けなかったアナタは、この下をじっくり読んでみてください。

一般的な解き方は

　まずは一般的な解き方を見てみましょう。小学校で習う筆算ですね。2桁×2桁は筆算で行うのが主流です。

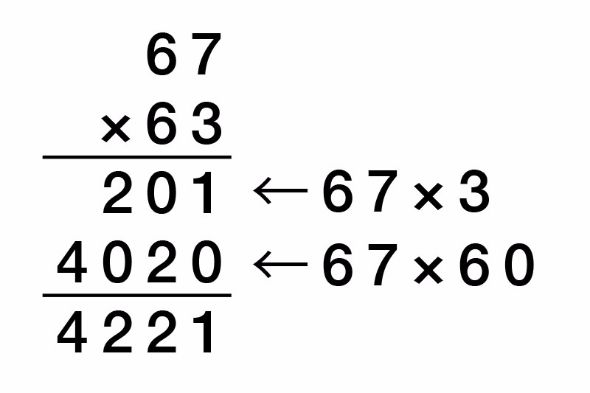
　小学校で習うこの筆算は、67×63を、（67×3）＋（67×60）として計算しています。この方法では、5秒で解くのは厳しいですよね。

ヴェーダ数学とは

　そこで「ヴェーダ数学」の登場です。ヴェーダ数学とは、古代インドの聖典『ヴェーダ』によって伝えられたとされる計算法。この方法を用いると、67×63は次のように考えます。

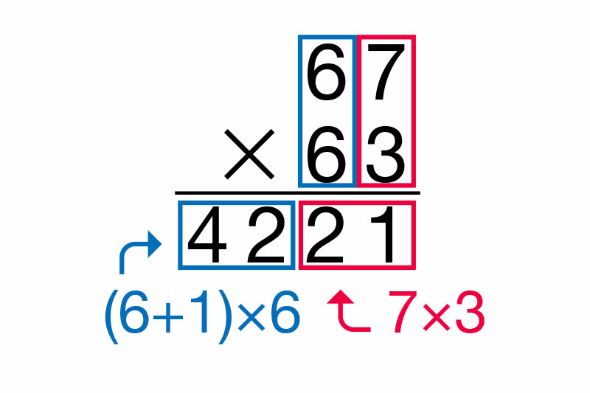
　えっ？　何これ？　どういうこと？

　言葉で書くとこんな感じの計算をしています。

• 答えの一の位と十の位は、計算式の一の位同士の掛け算
• 答えの百の位から上は、計算式の十の位に1を足した数に元の数字を掛ける

　つまり、この式では（6＋1）×6＝42の右に7×3＝21を書けば終了です。瞬殺！

　ここまで読んで、察しの良い方は分かったかもしれませんが、この方法で解くには次のような条件があります。

• 2つの数の、十の位が同じであること。2つの数の、一の位を足すと10になること

　つまり、「38×32」とか、「79×71」とか「94×96」とかであれば使える、ということです。ん、どういうことだ……？

仕組みを解説

　というわけで、どういう仕組みでこれが成り立つのか考えてみましょう。

　数学的に考えるには、文字に置き換えるのが一番なので、そうします。ここからは、ちょっぴり高校数学を使います。しばらく計算から離れていた大人たちは、頑張ってついてきてくださいね。

　（1）　67＝60＋7　→　6＝a、7＝bとすると　10a＋bとなる。

　（2）　63＝60＋3　→　6＝a、3＝cとすると　10a＋cとなる。

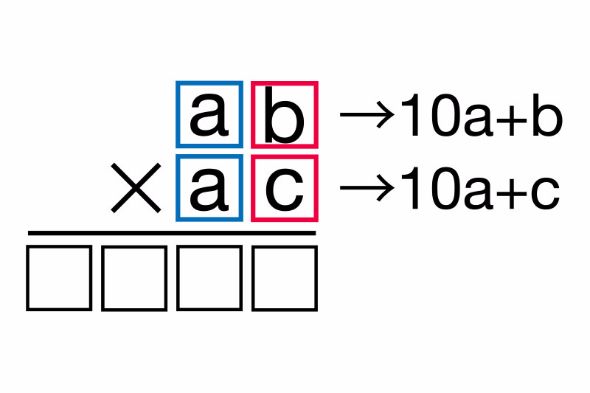
　これで置き換えが完了しました。

　続いて、67×63を、文字で表して、どんどん計算していきましょう。

　（3）　67×63　→　（10a＋b）×（10a＋c）と書ける。

　（4）　（10a＋b）×（10a＋c） ＝ 100a^2＋10ac＋10ab＋bc

　（5）　（4） ＝ 100a^2＋10a（b＋c）＋bc

　ここで、この計算の条件を思い出してください。

　“一の位を足すと10になること”とありましたね。

　つまり、この計算では　b＋c＝10　となります。

　（6）　（5） ＝ 100a^2＋10a×10＋bc

　（7）　（6） ＝ 100a^2＋100a＋bc

　（8）　（7） ＝ 100a（a＋1）＋bc

　おっ？　きれいにまとまった？

　ここで、元の計算を思い出してください。

　“（6＋1）×6＝42の右に7×3＝21を書けば完了”でしたね。

　これを、きちんと書くと、（6＋1）×6×100＋7×3です。

　（8）を見ると……あっ、合ってる！

　a（a＋1）にかけられている100は、a（a＋1）が百の位に書かれることを意味しています。

　つまり、a×（a＋1）の右にb×cを書けばいいというのは、a×（a＋1）に100がかけられているからだったんですね。

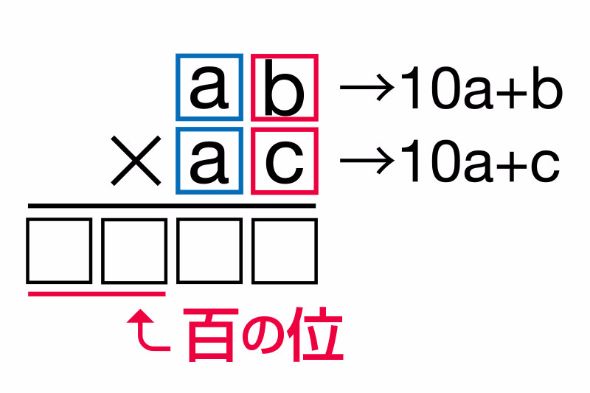
　きちんと考えてみると、67×63がなぜ5秒で解けるのか、納得できますね。

注意点もある

　注意しなければならないのが、一の位が1と9のとき。

　1×9＝9ですが、このときばかりは、ただ横に並べるのではなく、9を09と書かなければなりません。そこだけ注意してください。

まとめ

　さあ、最後に復習です。2つの数の、十の位が同じであり、一の位を足すと10になるときは

• 一の位と十の位は、一の位同士の掛け算
• 百の位から上は、十の位に1を足した数に元の数字を掛ける

　それでは最後に3問！

• 15×15＝？
• 49×41＝？
• 82×88＝？

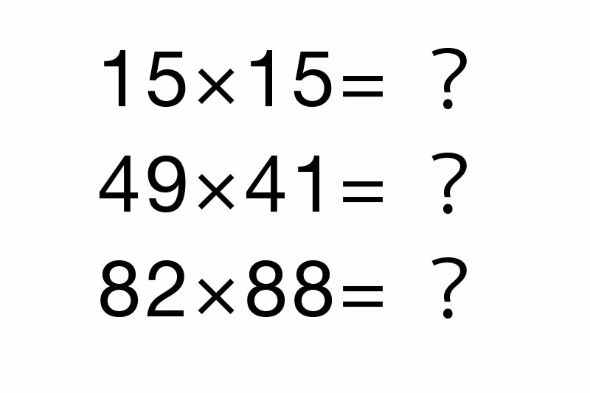
　答えは、上から順に225、2009、7216でした。

　使える計算式は限られていますが、覚えておいて損はないと思います。

　これに当てはまる計算であることに気が付いたら、一瞬で解けてうれしいですね。算数って楽しいなー。

制作協力

QuizKnock