大人になって解いてみると、意外と難しい。
思春期の象徴たる「中2」……。そんな中2で習った授業の内容を紹介しつつ、「こんな問題やったなぁ」とオトナたちが感傷に浸れるかもしれない「中2なら秒で分かるかもしれないクイズ」。
今回は中2なら余裕で分かるハズ? 「中1数学」からの出題です。
advertisement
問題
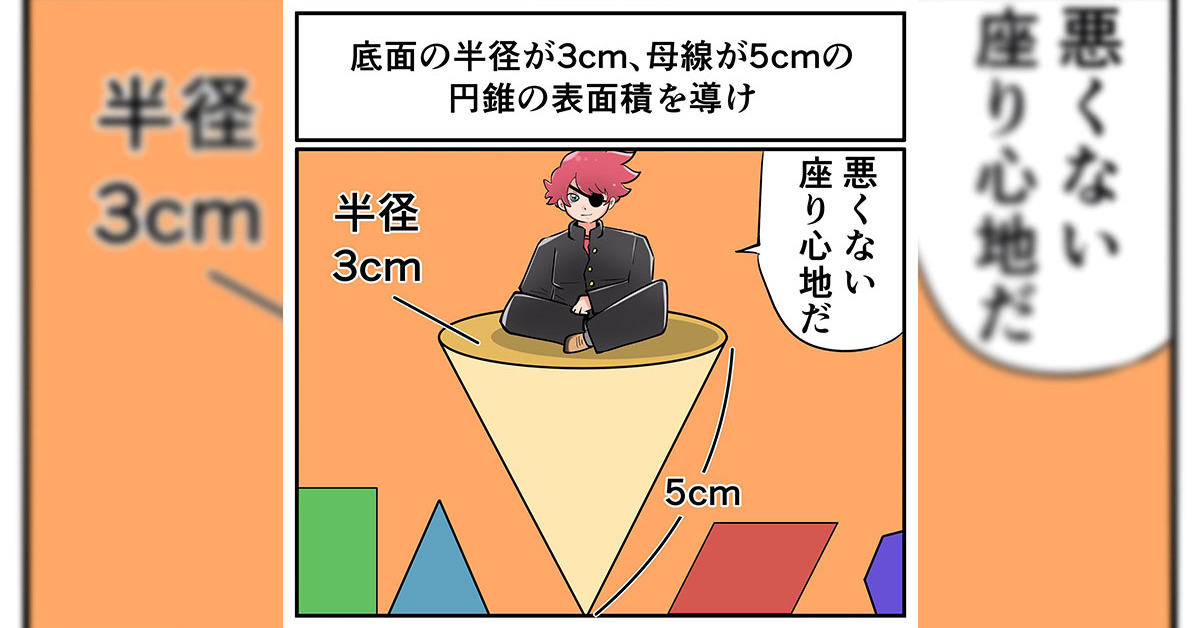
底面の半径が3センチ、母線が5センチの円すいの表面積を導け。
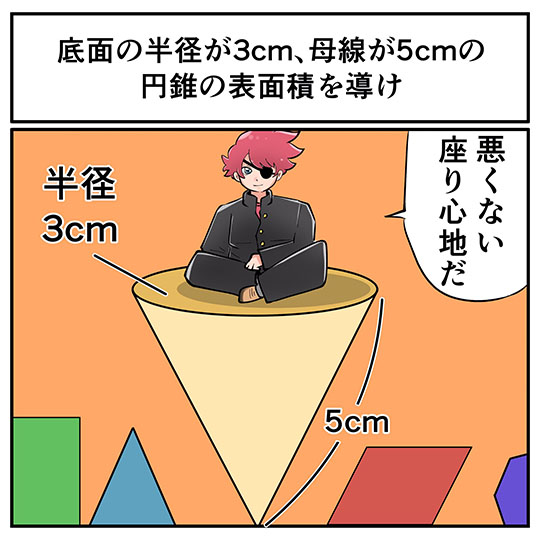
「円すいの上にも三年……」(イラスト:野田せいぞ)
今回は、中1の数学で学ぶ「空間図形」からの問題。円すいの表面積って確か……すごく簡単な公式があったような……?
さて、答えは分かりましたか。最後に答え合わせをどうぞ。
advertisement