できたら、かっこいい。
“パズル的”な解法で解くことのできる、五等辺六角形の角度を求める問題にチャレンジしてみましょう。ちょっと難易度は高いかも……?
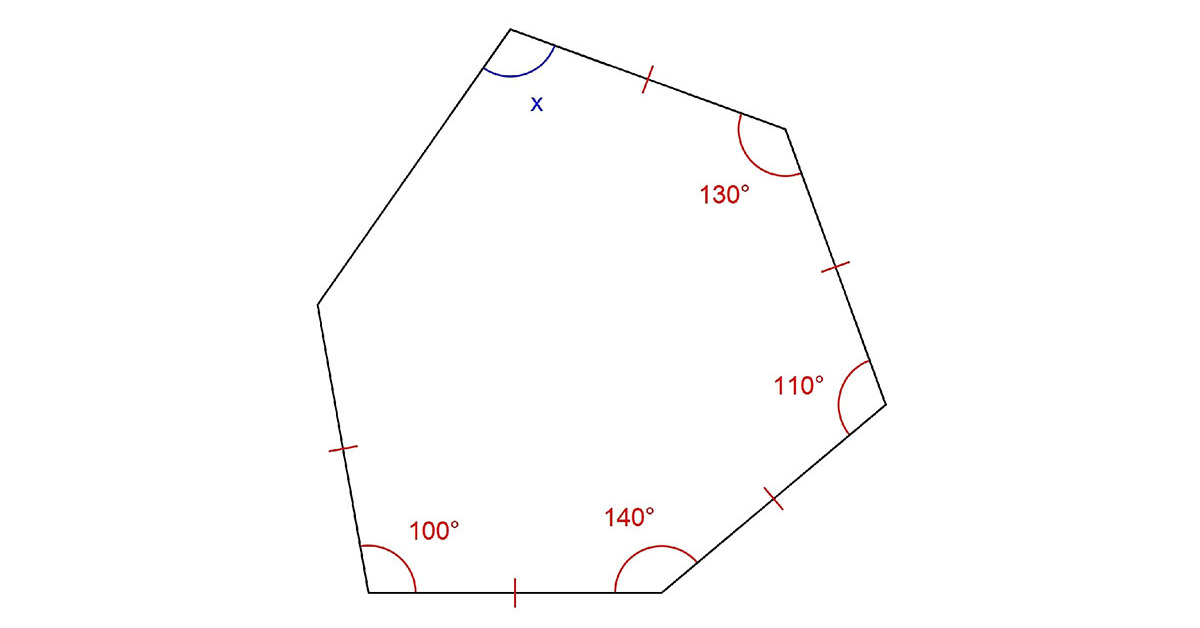
問題を作成したのは、Twitterユーザーのポテト一郎(@potetoichiro)さん。投稿されたのは、6本の辺のうち5本の長さが等しい五等辺六角形のイラストで、6つの角のうち等しい辺の間の角の大きさだけが分かっている状態です。これだけの情報からxの角度を求めてみてください。
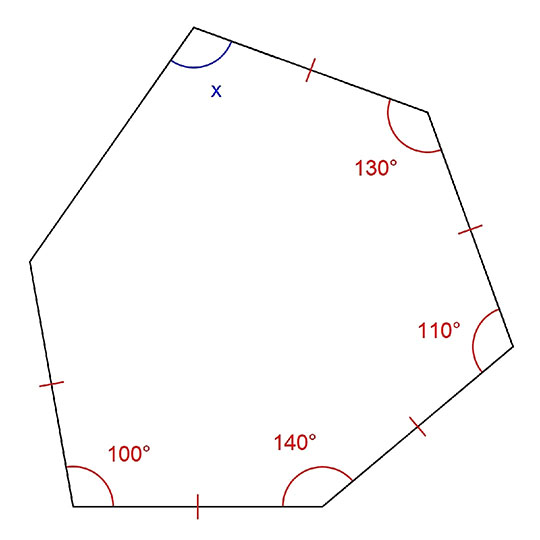
問題。難しい……
xを含む2つの角が分からないので、このままでは答えを求められません。とすると、補助線を引くしかありませんが……どうやって引けばいいの?
さあ、答えは分かりましたか? 分からない人はヒントを見てみるのもいいかもしれません。分かった人は答え合わせをどうぞ!
advertisement