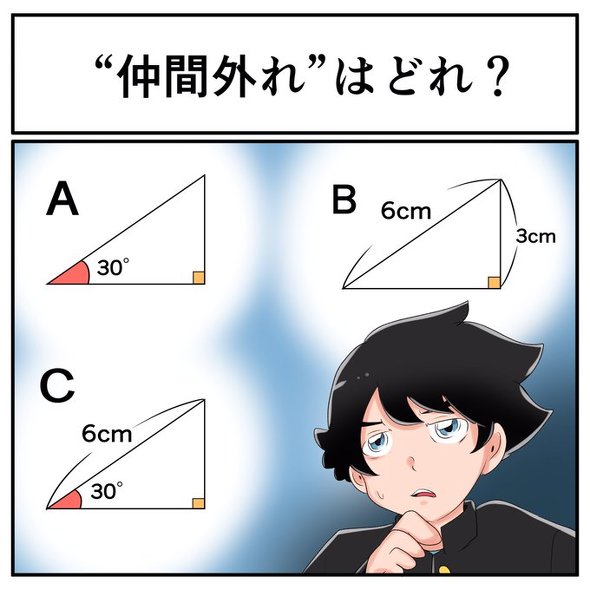
問題
答え
正解は「3/2」でした!
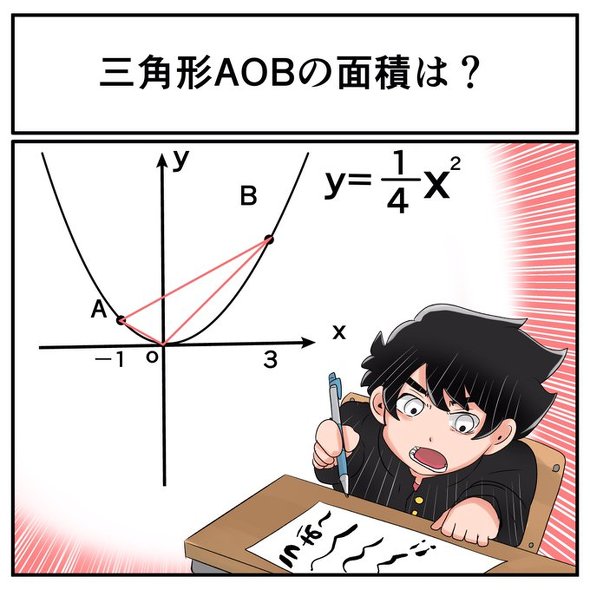
【解説】まずは、点Aと点B(と点O)の座標を求めます。点Aと点Bのx座標は−1と3なので、y座標はそれぞれ「(1/4)×(−1)2=1/4」と「(1/4)×(3)2=9/4」。よって、点A、B、Oの座標は以下のようになります。
- A(−1,1/4)
- B(3,9/4)
- O(0,0) ※原点
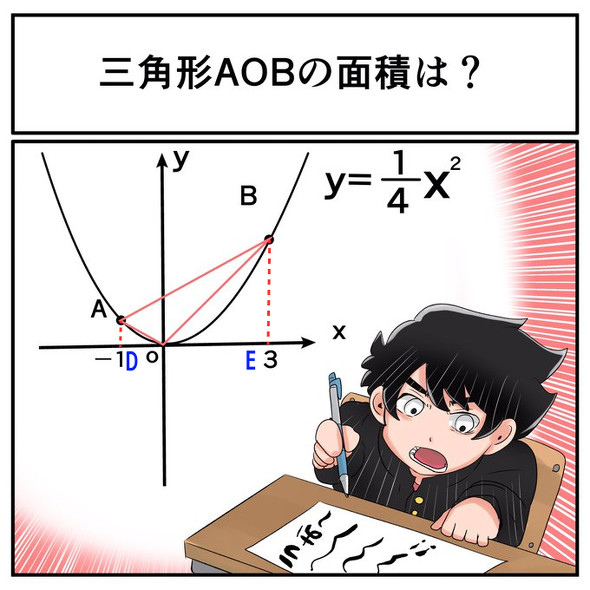
さらに、点A・点Bのそれぞれからx軸に下ろした垂線とx軸との交点を点D・点Eとすると、それらの座標は次のようになります。
- D(−1.0)
- E(3,0)
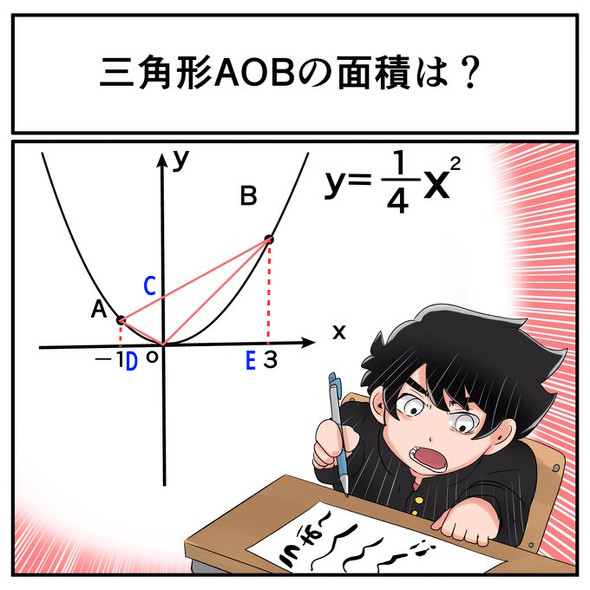
解法1:三角形AOBを2つに分割
直線ABとy軸の交点をCとすると、三角形AOBの面積は「三角形AOC+三角形BOC」で表せます。このとき、三角形AOCと三角形BOCは高さがそれぞれ「DO=1」「EO=3」と判明しているので、共通する底辺であるCOの長さが分かれば面積を出すことが可能です。そこでCの座標をC(0,b)とすると、底辺の長さはbとなります。
直線ABの式を求めましょう。直線の傾き(変化の割合)は「yの増加量/xの増加量」で求められるので、直線ABの傾きは「(9/4)−(1/4)/3−(−1)」つまり「1/2」です。よって、このとき直線ABの式は「y=(1/2)x+b」と表せ、これに点Aの座標を代入すると「1/4=(1/2)×(−1)+b」すなわち「b=(1/4)+(1/2)=3/4」となります。
したがって、三角形AOBの面積は以下のようになります。
三角形AOB
=三角形AOC+三角形BOC
=(3/4)×1×(1/2)+(3/4)×3×(1/2)
=(1+3)×(3/4)×(1/2) ※分配法則の逆「a×c+b×c=(a+b)×c」を利用
=4×(3/4)×(1/2)
=3/2
解法2:台形から三角形を除く
三角形AOBの面積は「台形ADEB−(三角形ADO+三角形BEO)」という式で求めることが出来ます。AD=1/4,DO=1,BE=9/4,EO=3,DE=4から、それぞれの面積は次のようになります。
- 台形ADEB=(AD+BE)×DE×(1/2)={(1/4)+(9/4)}×4×(1/2)=5
- 三角形ADO=AD×DO×(1/2)=(1/4)×1×(1/2)=1/8
- 三角形BEO=BE×EO×(1/2)=(9/4)×3×(1/2)=27/8
よって、三角形AOBの面積は以下のようになります。
三角形AOB
=台形ADEB−(三角形ADO+三角形BEO)
=5−{(1/8)+(27/8)}
=5−(7/2)
=(10/2)−(7/2)
=3/2
おすすめ記事
ねとらぼのクイズ記事
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
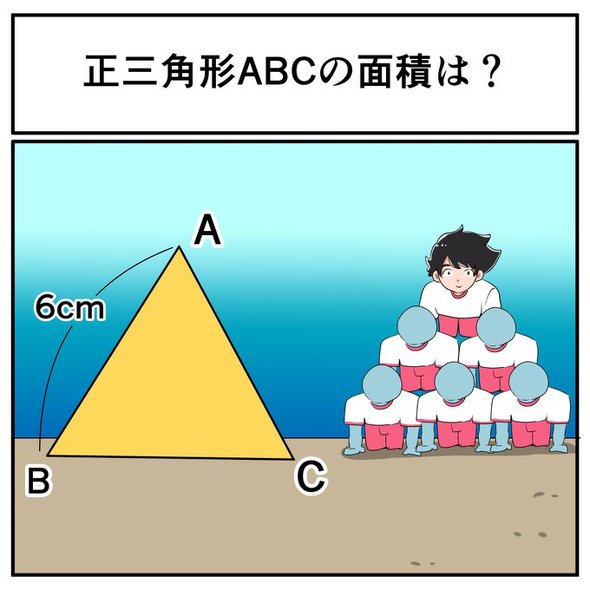
 1辺の長さが6センチの正三角形の面積は? 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
1辺の長さが6センチの正三角形の面積は? 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
大人になって解いてみると、意外と難しい。 この中に「仲間外れの三角形」が隠れています 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
この中に「仲間外れの三角形」が隠れています 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
大人になって解いてみると、意外と難しい。 三角形の内角の和はどうして180度なの? 中2なら秒で分かるかもしれないクイズ【数学・図形の性質】
三角形の内角の和はどうして180度なの? 中2なら秒で分かるかもしれないクイズ【数学・図形の性質】
大人になって解いてみると、意外と難しい。 121の平方根を求めよ 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
121の平方根を求めよ 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
大人になって解いてみると、意外と難しい。 「x^2+3x+2=0」を解け 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
「x^2+3x+2=0」を解け 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
大人になって解いてみると、意外と難しい。