「テストで電卓使ってもいいよ！」 日本と米国の数学、考え方の違いとは？

どこに頭を使うのか。

[QuizKnock，ねとらぼ]

　皆さんの中には数学が「好きで得意！」という人も、「嫌いで苦手！」という人もいると思う。後者の多くは数学が難しいと感じているはずだ。

　日本の義務教育は9年間。年々学ぶごとに抽象度を増していき、中3にもなると「平方根」「2次方程式」「図形の証明」……などなどの壁が待ち受ける。早い人はここで数学嫌いになってしまうだろう。

　高校へ進学しても「指数関数・対数関数」「三角関数」「微分・積分」……と、数学嫌いの心をへし折る難関が続く。

　日本の数学教育ではこれだけ多くのことを学ぶわけだが、実はこれは国際的に見ると結構難しい部類に入るのだ。

　今回は、米国の大学入試を比較対象に、数学の内容の違いを見てみる。

米国の入試ってどんなもの？

　日本の大学入試、特に推薦やAOでない一般入試は、

• センター試験（全国共通）
• 大学ごとの個別試験

　のいずれか、または両方の成績から判定されることが多い。

　米国の場合は大きく違っていて、一般には試験は「SAT」という全米共通の標準テストのみ。

　その他、高校の成績や小論文などを提出し、それらを総合して判定される。

SAT（標準テスト）てなに？

　従って、大学に進む米国の高校生は、最低限SATの内容をマスターしているはずだ。

　SATには、読み書きと数学から判定する論理テスト（SAT I）と、科目別に実施される科目別テスト（SAT II）の2種類があり、一般に用いられるのはSAT Iのほうだ。

　SATを実施している機関から、米国の受験生向けにガイドが公開されているのでここで読んでみよう。

　SATの数学が日本の試験と大きく異なる点は、SATの場合電卓の持ち込みができること。「電卓を使わないで解く問題」と「電卓で解く問題」が用意されており、「電卓で解く問題」にはグラフが表示できる程度の高機能な電卓が持ち込める（四則演算しかできない電卓は「推奨しない」とまで書いてある）。

　つまり、単純な計算力よりも答えを出すための思考力を重視していることが分かる。

難しそうに見えるけど……

　受験生向けのガイドには例題も載っている。解いてみよう。

　まず表紙を見ると、Reference（参考）が親切で驚く。

出典：SAT Suite of Assessments

　面積や体積の公式、さらには「三角形の内角の和は180度ですよ」とまで書いてある。これらを覚えているかではなく、これらがちゃんと使えれば十分だという認識なのだろう。

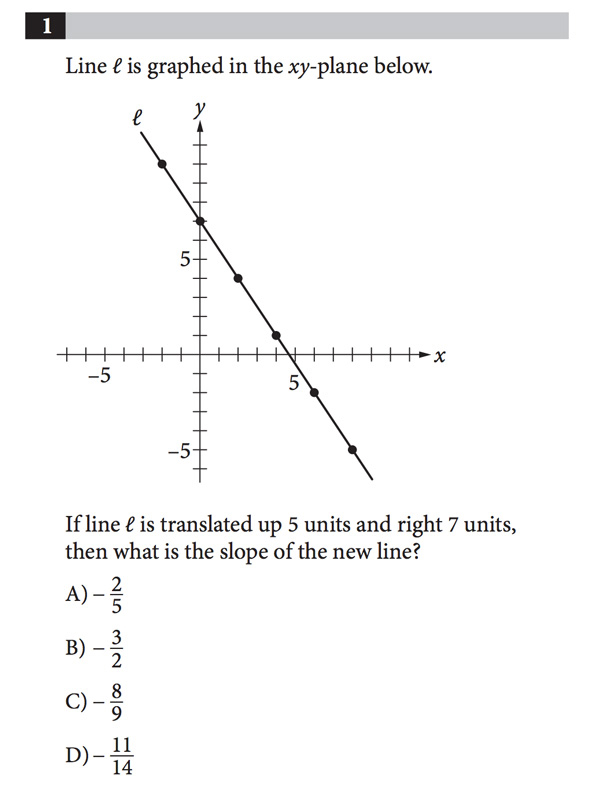
　まず1問目。Estimated Difficulty（予想難易度）はEasy（簡単）と書いてある。

出典：SAT Suite of Assessments

　「直線lが下のxy座標に描かれています。直線lを上に5、右に7だけ動かしたとき、新しい直線の傾きはいくつでしょう？」

　直線を動かしているのでややこしそう……と思いきや、求められているのは傾き。直線の傾きは平行移動では変化しないので、図から傾きを求めればよく、正解はBだ。

　次は「電卓で解く問題」から、予想難易度Medium（普通）の5問目を見てみる。今度は図形の問題だ。

出典：SAT Suite of Assessments（https://collegereadiness.collegeboard.org/）

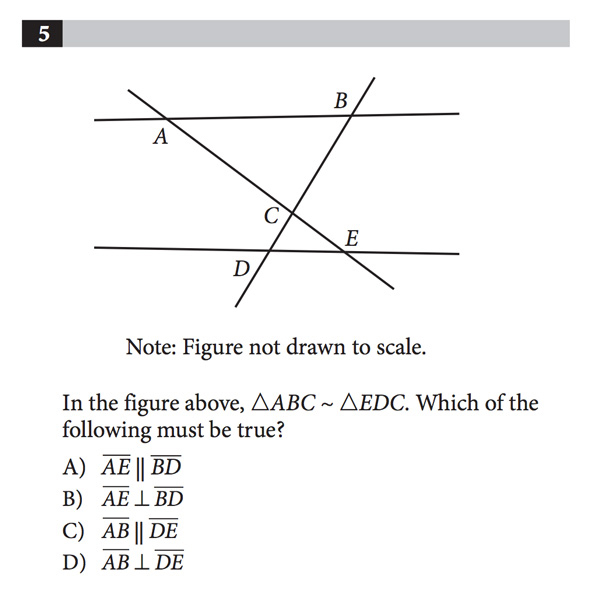
　「上の図で、ΔABC∽ΔEDC（∽は相似を表す記号）です。次のうち必ず正しいのはどれでしょう？」

　「||」は2本の直線が並行であることを表す記号で、日本だと「//」で習う。2直線が垂直であることを示す「⊥」の記号は日本と同じだ。

　相似な2つの三角形から∠BACと∠DECは等しい。この2つは錯角の関係にあるので、直線ABとDEが平行であることが分かる。正解はCだ。これも日本では中学校の数学で習う範囲だ。「電卓で解く問題」にも、電卓がなくても解けそうな問題は出てくるようだ。

　最後は「電卓を使わない問題」の5問目。予想難易度Hard（難しい）はいかほどか？

出典：SAT Suite of Assessments

　sin（π/5）と等しい三角関数を選ぶ問題。これはさすがに少し難しい……。sin（π/5）もcos（π/5）も正の数なので、AとBは等しくなるわけがない。cos（θ）=sin（θ+π/2）で求められるので、Cのcos（3π/10）はsin（4π/5）に等しい。sin（θ）=sin（π-θ）なので、sin（4π/5）=sin（π/5）。よってCが正解だ。

　例題を3問見たが、他の例題を見ても超難問は見当たらない。センター試験の数学よりは簡単そうだ。

　特に、日本では高校で学ぶ「微分・積分」は一切出題されていない。米国は州ごとに教育制度が異なるので一概にはいえないが、高校レベルでは数学の基本をしっかり覚え、今後の進路で数学が必要な人のみ、より高度な数学を学ぶというシステムなのだろう。

入学後がまた大変だ

　ここまで見てきたように、米国の標準試験は、数学に限ってみれば日本よりかなり簡単に思える。

　なら日本人ならハーバード大学でも余裕で入れるの？　というともちろんそんなことはない。合否の判定には高校での成績や課外活動が重視され、勉強だけできても合格できないらしい。

　さらに、いざ合格して入学できても、待っているのは日本とは比べものにならない厳しい単位認定……。卒業に至る難易度は、日米で大きな差があるといわれている。

　これらは教育制度の歩み方から生まれた違いであり、どちらが良い悪いと一概に決められるものではないだろう。今、日本ではセンター試験に代わる「学力評価テスト」の形式が議論されている。日本のスタイルをどれだけ残し、海外の手法をどう取り入れるのか。これこそまさに、答えを出すのが難しい問題だ。