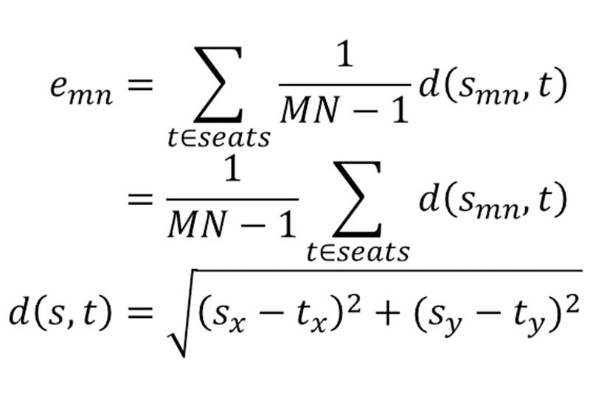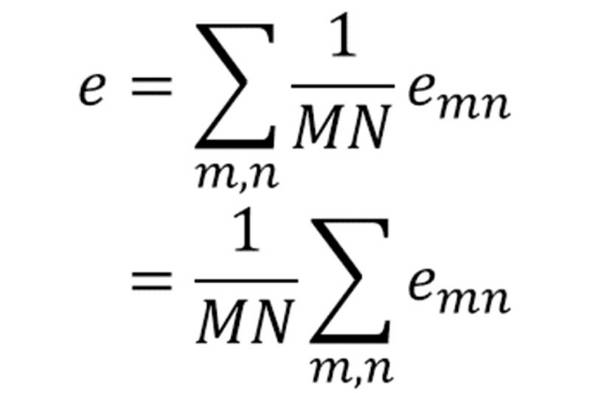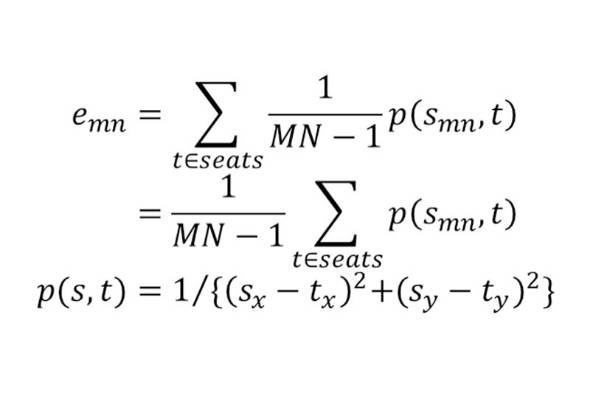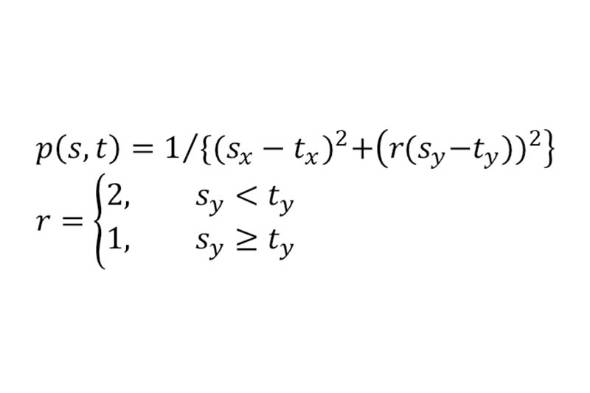クラス内で「最も恋が成就しやすい席」はどこか、科学的に分析する

このクラスで一番の美人との距離はどのくらい？

[QuizKnock，ねとらぼ]

　春、それは出会いの季節だ。きっと新たな恋も生まれることだろう。

　学校では定期的に席替えが行われる。大抵はくじ引きなどで新しい席を決めると思うが、気になる人が近くになるとうれしい。

　それなら、気になる人はどのくらいの確率で近くに座ってくれるものなのだろう？　ちょっと分析してみたい。

距離の期待値

　前提として、クラスにはN人の列がM列あり、M×N人の生徒がいるとする。また、男女関係なく同じくじを引き、いずれの席も同じ確率で当たるものとする（男女別の列にする席替えもよくあるけど）。

　席替えで好きな人の近くに行きたい……ということで、自分と特定の1人との間の距離の期待値を考えてみる。数学の問題として出てくると少しウッとなる設定だが、落ち着いて考えれば大丈夫。

こんな感じで計算していく（読み飛ばしてよい）

　自分の位置（MN通り）が決まっているとして、好きな人がほかの（MN-1）つある席のどこになるかは、等確率1/（MN-1）で決まる。期待値の定義通りに計算していくと、次のように「各席におけるあの人との距離」の期待値が求まる。

e（添字は席の位置）は各席における気になる人との距離の期待値、d（s,t）は2つの席s（教室の横方向にs_x、縦方向にs_yの位置にある）、t（sと同様）間の距離。

　MN通りの自分の位置はそれぞれ確率1/MNで現れるので、このクラスで席替えしたときのあの人との距離の期待値は次のように求まる。

具体的には……

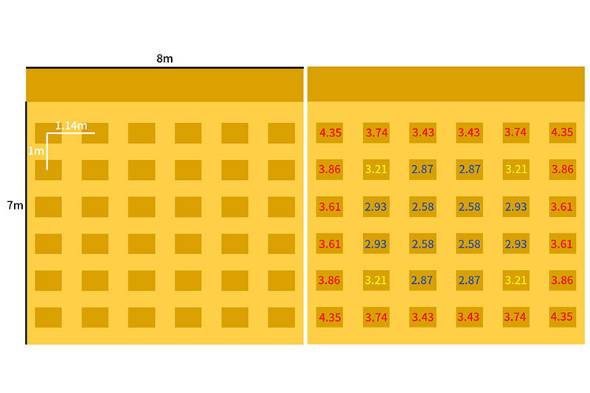
　文字ばかりだとピンと来ないので実際にやってみる。8m×8mの教室に36人が6人ずつの列を6列作って座っている場合を考える。前方は教卓で1mほどスペースがとられるとすれば、横の列間は1.14m、前後の間は1m。

　このとき、「各席におけるあの人との距離」の期待値は次のようになる（計算量が多いのでプログラムで直接計算した）。

　結果として、教室の中心付近はあの人が周囲に来る確率が高く、期待値も従って小さくなる。

　これらの平均をとることで全体の期待値が求まり、期待値は3.40。「8m×8mの教室において、好きな人とは平均して3.4m離れる」ということがいえる。また、値がこれより大きいクラス席は内側の席よりも想う人が遠くになりやすい。クラスの端の席を引いたらガッカリだが、西片も後ろの席で高木さんの横を当ててるわけだし希望はある。

離れたくない

　しかし、単純な距離による評価では実感に反する気がする。例えば、気になる子が自分のすぐ隣の席に座るのと、そのさらに隣の席に座るのでは、距離では2倍の差だが実感は3倍も4倍も違うはず。

　アメリカの心理学者ボッサードも、二者の距離が近いほうが恋愛感情が生まれやすい（ボッサードの法則）ことを実証している。遠距離恋愛は実りにくいのだ。

　そこで、距離が小さくなると評価が上がり、離れるにつれて著しく評価が下がるようにしてみたい。

　ここで評価基準を「2つの席の間の距離の2乗の逆数」と定める。これは、万有引力や磁力などの大きさが距離の2乗に反比例する力に習ったものだ。恋は引力だからね。

　それから、気になる子が自分の後ろにいるよりは、前のほうに座っていて後ろ姿が見えるほうがいい。従って自分より後ろの席の評価は下方修正すべきだろう。

　よって、評価式の中の距離の前後成分に関して、自分より後ろの席の場合には係数をかけて評価を落とすことにする。今回は係数を2とした。

位置の前後成分（y軸方向）に係数rをかけ、相手が後ろにいるときは距離を大きくして評価を落とす。rの値は何でも良いが今回は2とした

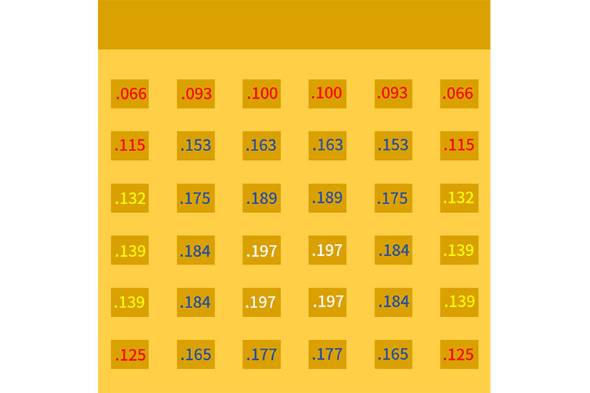
　これを用いて、先ほどと同様の例で各席の評価の期待値を求めてみた（先ほどは「距離」の期待値なので小さい方がよく、今回は「評価」の期待値なので大きい方がよい）。これらの数字の平均をとって、このクラスにおける評価値の期待値は0.15となる。

　列の中で比較すると、後ろの席で評価値が高い傾向がみられるようになり、より実感に即した値に近づいたと思う。最前席は当然前に席がないので評価が低い。先生にも常に見られるし本当に良いところがない。

　主人公が座っていそうな窓側後ろから二番目席もそこまで評価は高くない。クラスの中心人物がいそうなゾーンでいい値が出ている。

あの娘との恋愛に最適な教室内配置は？

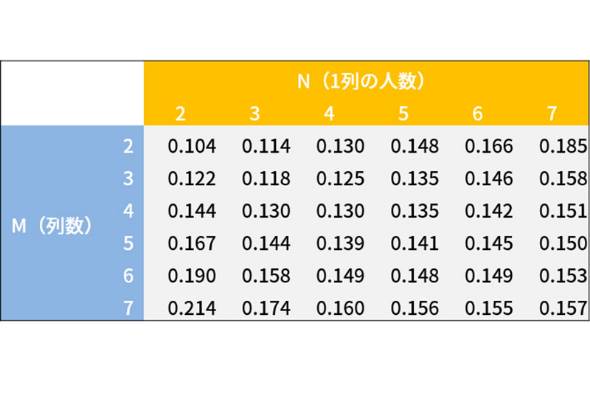
　最後に、M（列数）とN（1列の人数）を変化させたときの評価値の期待値をそれぞれ調べてみた。

　同じ人数で違う配置、例えば24人クラスで4列と6列を比較した場合、わずかながら列数が多い（1列当たりの人数が少ない）ほうが期待値が高くなることが分かる。これは列数が多いと有利（？）な後ろの席が増えるからだと思われる。クラスの席配置を決める立場の先生方は参考にしていただきたい。

恋の行方は……

　いろいろ書いてきたが、これを読んだところで席替えが有利になるわけではないのである。結局は天に任せるしかないから。

　これを読んだ方が新たな環境で恋を咲かせることを願う。方法は知らない。自分が咲かせられたことがないから……。

制作協力

QuizKnock