東京の開成中学校、兵庫の灘中学校……中学受験をしたことがない人でも一度は聞いたことのある有名な中学校の入試問題は、「これ本当に小学生が解くの……?」と驚いてしまう難問ぞろいです。
今回は千葉県の有名中学校である市川中学校の入試問題に挑戦してみましょう。
問題
次の2つから地球の円周を求めなさい。
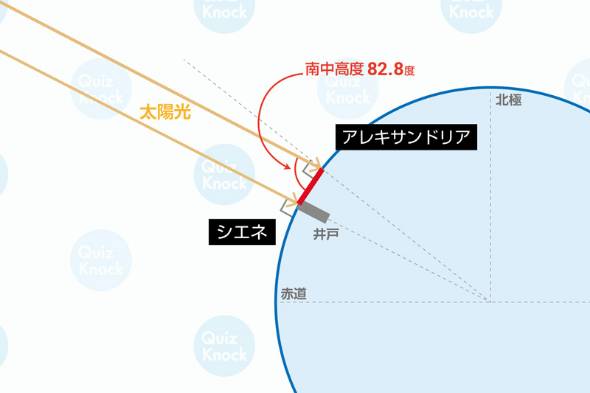
1.夏至の日、エジプトのシエネではとても深い井戸でも底まで太陽光が届いた。
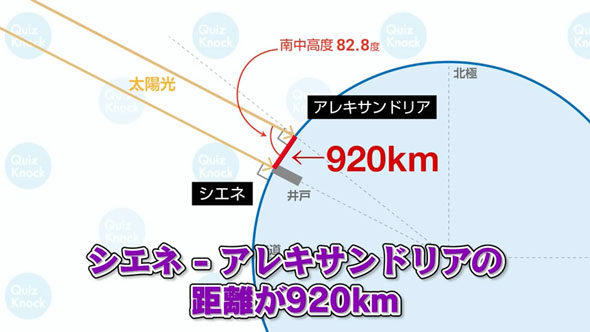
2.同じ日、シエネより920km北にあるアレキサンドリアでは、太陽の南中高度は82.8度である。
平成29年度市川中学校入試問題・改題
紀元前3世紀、古代ギリシャの数学者エラトステネスが、世界で初めて地球の大きさを計算しました。エラトステネスが上の条件からどうやって地球の円周を導き出したのかを考える問題です。
ちなみに南中高度とは、北半球において、一日で太陽が一番高く登ったときに地上から見上げる角度です。
解説
まず、問題文にある「1.夏至の日、エジプトのシエネではとても深い井戸でも底まで太陽光が届いた」とは、南中高度が90度であることを意味しています。
ここで、シエネとアレキサンドリアの距離と南中高度の差をそれぞれ出します。
- シエネとアレキサンドリアの距離:920km
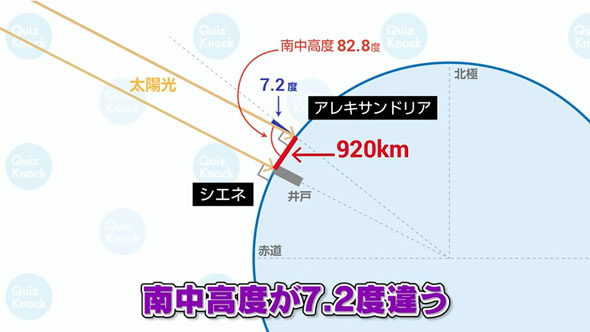
- シエネとアレキサンドリアの南中高度の差:90度ー82.8度=7.2度
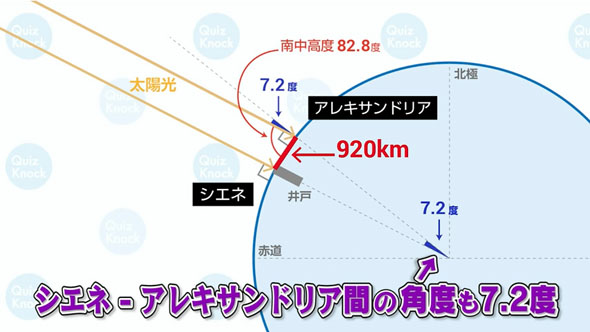
太陽光は地球のどの位置にも平行に降り注ぐので、上で求めた南中高度の差7.2度は上図の通り、シエネとアレキサンドリア間の扇形の角度と等しくなります。(平行線の同位角)
よって、比の計算を用いて
- 920km:7.2度=地球の円周:360度
- 地球の円周=46000km
シエネとアレキサンドリア間の情報、平行線の同位角、南中高度といった条件を整理し答えを導く問題でした。
これを小学6年生が解くわけです。日本の未来は明るいといえるのではないでしょうか。
ちなみに、現在では地球の円周は約4万kmと知られています。エラトステネスはGPSもPCもないはるか昔に実際の数値と誤差が15%しかない値を求めることができた大天才だったわけですね。
詳しい解説はこちらからどうぞ。
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
 「40−32÷2=?」この問題、解けますか?
「40−32÷2=?」この問題、解けますか?
理系にはすぐ解けて、文系には解けない、とんち問答のような問題がネットで話題に。 これ12歳が解けるの!? 超難関「灘中学」の入試問題「初日の出を2回見るには?」を解いてみた
これ12歳が解けるの!? 超難関「灘中学」の入試問題「初日の出を2回見るには?」を解いてみた
あなたは最強小学生に勝てるか? 21年前のワープロ「書院」で2018年にインターネットをしたら、無間地獄に突入した
21年前のワープロ「書院」で2018年にインターネットをしたら、無間地獄に突入した
ネット機能を搭載した21年前のワープロで、2018年のネットの世界を見てみました。 「16×4は?」「68−4だから64」 小学1年生の掛け算の計算方法が斬新だと話題に
「16×4は?」「68−4だから64」 小学1年生の掛け算の計算方法が斬新だと話題に
発想が見事。 「カニミソ」はカニの何なのか?
「カニミソ」はカニの何なのか?
カニミソって何だ? 脳ミソか? 僕は何を食べようとしているのだ?