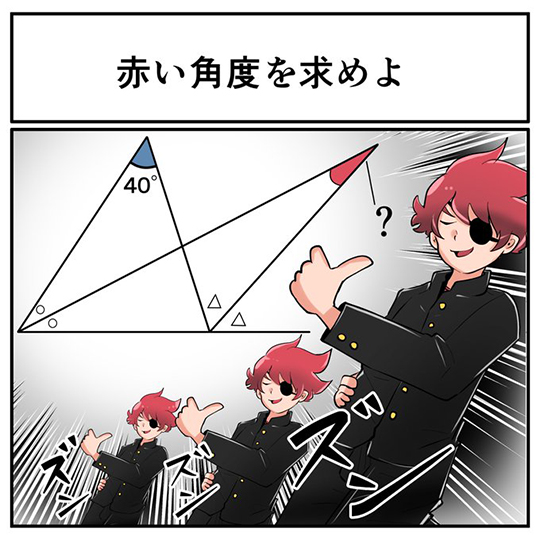
大人になって解いてみると、意外と難しい。
思春期の象徴たる「中2」……。そんな中2で習う授業の内容を紹介しつつ、「こんな問題やったなぁ」とオトナたちが感傷に浸れるかもしれない「中2なら秒で分かるかもしれないクイズ」。
今回も「数学」からの出題です。
advertisement
問題:0〜4の5枚のカードから3桁の数字を作るとき、3の倍数になる確率は?

「この勝負、必勝法があるのさ……」(イラスト:野田せいぞ)
今回は、中2の数学で学ぶ「確率」からの問題。3の倍数になる条件が分かればすぐ答えが分かりそうですが……落とし穴に気をつ付けて(関連記事)。
さて、答えは分かりましたか。最後に答え合わせをどうぞ。
advertisement
過去の「中2なら秒で分かるかもしれないクイズ」
<!–info end–>