おっぱいでわかる微分の使い道

学校で習いたかった。

[QuizKnock，ねとらぼ]

　高校数学で習う微分。積分とセットで習うあれ。「習ったけど意味はわかっていない」「取りあえず文字の右肩の数字を左に下ろしてた」……そんな人も多いのでは。

　そこでこの記事では微分について、何の意味があるのか真面目に解説する。皆さんも正座して真剣に読んでほしい。

微分の基本

　まず、微分が一体何なのか確認しておこう。数式は出てこないのでイメージをつかんでもらえればOK。

　微分は、曲線や曲面の傾き具合を知るための操作である。具体的にどうやっているのか、図で追ってみよう。

「傾きを知りたい点（赤）」と「少しずらしたところの点（青）」を結ぶ直線。求める傾きよりもゆるい

青い点を左にずらしていく。本当の傾きに近づいてきた

重なった！　ここ！　これだよこれ！

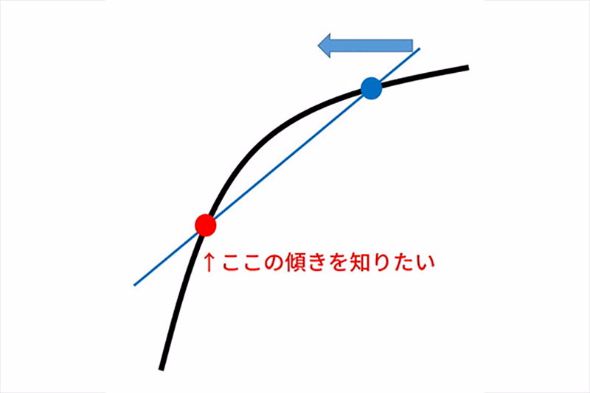
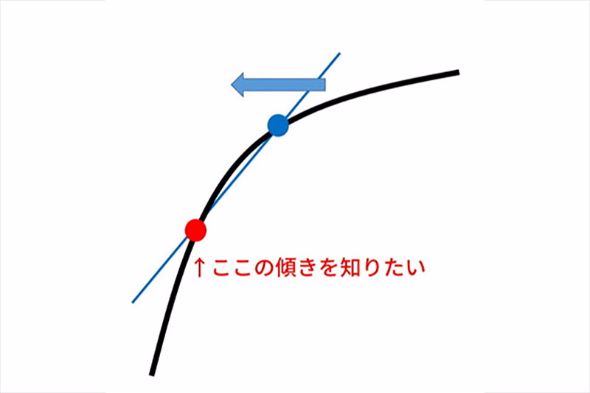
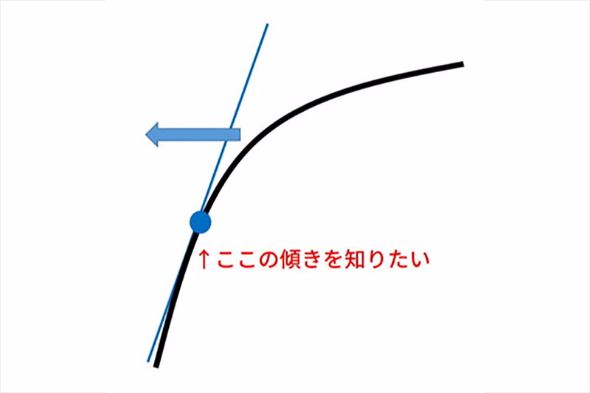
　このように微分は、曲線上の2点を近づけていくことで接線（曲線に接する直線）の傾き具合を知る操作なのである。

　傾きがわかると、その関数の「増え方」がわかる。急な斜面を登っているときは、一歩ごとに標高もグングン上がっていく、という感じだ。

　この標高の上がり具合は、いろいろな調査に利用可能である。経済学なら、もうけを最大化するために雇うべき最適な人数がわかる、というように応用される。

例えば曲線の山の部分では接線が水平になる、すなわち傾きが0になる

曲線ではなく曲面でも

　高校数学では曲線（変数が1つの関数）の微分しか習わないが、曲面（変数が2つ以上ある関数）についても微分ができて、その結果は平面になる。

　とはいえ、曲面は平面上で表せないのでイメージしづらい。身近な曲面……そう、おっぱいで考えよう。

　本物のおっぱいはここでは見せられない。すまないが水信玄餅CGの球体を心の目で置き換えて見てほしい。

手を平面にして肌をなでていく

あくまで接することを意識して、押し付けずに優しく傾きを測る

傾きが大きい方向に接点をずらすと近づく（どこへとは言わない）

あ！　ここ！　ここ！（どことは言わない）

　例え暗闇でその形がわからなくても、接面たる手のひらを頼りに、わしづかみがクリーンヒットする位置を探ることができる。これが曲面（おっぱい）と接面（手）の関係だ。

真面目な記事です

　このおっぱいの頂点探しと同じような原理が、現実の真面目な場面でも用いられているのだ。

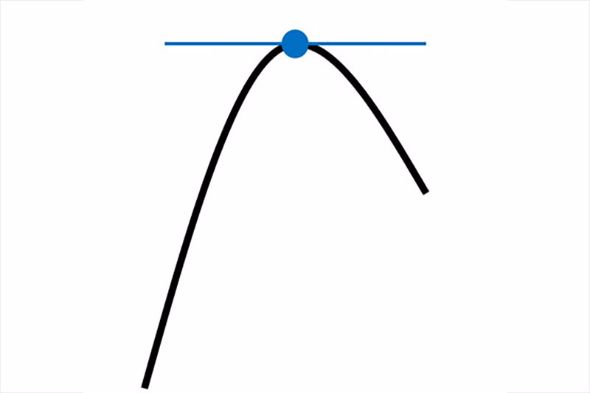
　ある関数（グラフにすると曲面になる）を最大にしたい、つまり曲面の一番盛り上がった部分を探したいとする。

　適当な位置からスタートして、関数を微分した結果が示す「傾きが急な方向」に進んでいけば、曲面が無限に高くない限りいずれ山にたどり着く。

　曲面の形によっては最大値が求まらないこともあるが、コンピュータで問題を解くときの基本的な考え方の1つである。ふざけていただけじゃないんだぞ。

まとめ

　数学を勉強するときは、ひたすら問題を解く前にいったん立ち止まり、やろうとしていることにどんな意味があるのか考えてみると、より理解しやすくなるはず。

　曲線がおっぱい、接線が手のひら。微分する前に思い出してね。

制作協力

QuizKnock