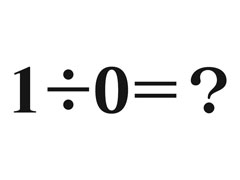小学生でもわかる「割り算で0で割ってはいけない」理由

小学生でもわかる考え方で説明してみました。

[QuizKnock，ねとらぼ]

　小学校の算数の授業で「1÷0=？」の答えをどのように習いましたか？

　1でしょうか？　0でしょうか？　それとも「答えはない」？

　結論から言うと1や0ではありません。しかし、「答えがない」と言い切ってしまうわけにもいきません。

いろいろな割り算の考え方

　まずは、基礎の復習から。割り算を理解するアプローチは、いくつかあります。

イメージから理解する

　「10÷5＝？」という計算は「10個のりんごがあります。これを5人で分けたら、1人あたり何個のりんごがもらえますか」という文章題に置き換えることが可能です。

　このように、ストーリーに置き換えると計算の意味が理解しやすくなります。

引き算から理解する

　次は、引き算から理解する方法。「10÷5＝？」を「10から5を何回引いたら、その数から5が引けなくなりますか」とする考え方です。

　電卓が開発される前に使用されていた手回し計算機は、実際にこのような仕組みで割り算を行っていました。

かけ算から理解する

　さらに、割り算の前に習うかけ算から理解することもできます。これは「10÷5=？」を「5×？=10となるとき、？に入る数はいくつですか」と理解するやり方です。

　上の2つが、余りの出る計算結果になるのに対し、この方法では分数を答えとして導くことができます。

1÷0=？

　それでは、最初の「1÷0=？」という計算をこれらの方法で考えてみましょう。

イメージ

　「1個のりんごがあります。これを0人で分けたら、1人あたり何個のりんごがもらえますか」

　あれ、そもそも人が存在しない!!

0人で分ける……？

　まったくわけの分からない問いになっており、問題文として成り立っていません。

引き算

　「1から0を何回引いたら、その数から0が引けなくなりますか」

　「1-0＝？」の答えが1であることは、誰の目にも明らか。よって、この場合は「何回でも無限に引ける」ということになります。

　ちょっと視点を変えて、引き算を足し算に置き換えるとどうなるでしょうか。

　たとえば「10から5を何回引いたら、その数から5が引けなくなりますか」という問題は「5を何回足したら10になりますか」と同じです。この場合、「5+5=10」なので、「2」が答えになります。

　これを「1から0を何回引いたら、その数から0が引けなくなりますか」に当てはめると、「0を何回足したら1になりますか」と捉え直すことができます。

　当然、0に0を何回足しても1にはなりません。つまり、この計算は「不可能」です。

かけ算

　「0×？=1となるとき、？に入る数は何ですか」

　そんな数は存在しません。かけ算として考えると「0を何倍したら1になりますか」と聞かれているわけですから、どう頑張っても「不可能」です。

　3パターンで考察したことで、「1÷0＝？」という計算には解がない（不能）であることが分かりました。これが「0で割ることはできない」ということなのです。

「0÷0=？」は違う理由で答えが出せない

　さて、今度は別の式で0の割り算を考えてみましょう。

イメージ

　「0個のりんごがあります。これを0人で分けたら、1人あたり何個のりんごがもらえますか」

どういう状況なんだ……

　意味が分からない文章題になってしまいました。「0÷0=？」も、この方法で考えるのはやめておきます。

引き算

　「0から何回0を引いたら、その数から0が引けなくなりますか」

　「0-0＝？」は当然、0です。答えは簡単に出ましたが、「0から0を引く」という考え方がアリなのか、ナシなのか怪しいところです。今回も足し算で考え直してみましょう。

　「0を何回足したら0になりますか」

　「0+0＝？」の答えは0。「0+0+0」も「0+0+0+0」も0です。

　つまり、0はいくら足しても0。何回と答えても正解なので、答えが1つに定まりません（不定）。

かけ算

　「0×？=0となるとき、？に入る数はいくつですか」

　「1×0＝？」の答えは0。「2×0」も「3×0」も0です。先ほどと同じ論法で、これも不定となります。

まとめ

　数学らしく話をまとめると

• a÷0のとき、a≠0であれば、答えは「不能」となる
• a÷0のとき、a=0すなわち、0÷0であれば、答えは「不定」となる

　という結論になります。

　QuizKnock編集部には「小学校の授業で『1÷0＝0』と習った」という人が実際にいました。子どもに説明するのはやや難しいところかもしれませんが、せっかく「÷0」の計算に触れるのであれば、誤解のないように教えてあげたいものです。

制作協力

QuizKnock