あなたのクラスに同じ誕生日の人がいた理由、数学的に教えます

確率を計算すると、驚きの結果が。

[QuizKnock，ねとらぼ]

　あなたは聞いたことがあるだろうか。「1つのクラスに必ず同じ誕生日の人が1組以上いる」という噂を……。

　うるう年の場合、1年は366日。1クラスあたりの学生数は、学校によって異なりますが、仮に40人だったとしましょう。

　この中で同じ誕生日のペアができるなんて、直感的には「運が良いと、そういう不思議なことも起こるよね」くらいの話にしか思えませんが……実際のところ、どうなのでしょうか。

余事象の確率

　噂が本当なのか、確率を使って考えてみましょう。求めるのは、40人のクラスに誕生日が同じ人がいる確率です。

　日数が366日で、クラスが40人であることから「この2つの数字で割り算すればいいのだろう。40/366を計算しよう」と単純に考えてしまうと、問題の本質を見誤ります。

　正解にたどり着くためのポイントは、問題の言い換え。誕生日が同じ人がいる確率を直接出そうとするのではなく、「全員が同じ誕生日に“ならない”確率を出してから、引き算すればいい」と捉えるのです。

　というのも、同じ誕生日になる確率とだけ言うと、同じ日に3人が被っている場合、誕生日が同じペアが2組ある場合など、とても多くの場合を考えなければなりません。しかし、余事象（知りたい出来事の反対の出来事のこと）の確率の考え方を使えば、全員が別の誕生日である確率を求めるだけでよいのです。

いざ、計算

　それでは、うるう年生まれの学年のクラス（40人）に、誕生日が同じ人がいない確率を計算してみましょう。

　まず1人目は366日のうちどの日付でもよいので、366/366 = 1 。つまり、1人のクラスだと誕生日が同じ人がいない確率は100％（全員の誕生日が違う）ということです。当たり前。

　2人目の誕生日は、1人目と違う日付です。すなわち、2人目の誕生日は366通りのうち、1人目の日付を除いた365通りしかありません。そこで、「366/366 × 365/366」を計算すると、答えは0.997。99.7％という高確率で、2人の誕生日が違うことになります。まあ、そうでしょうね。

　3人目でも同じことをして、366/366 × 365/366 × 364/366 = 0.992（99.2%）。この調子で40人分やれば完了です。暗算だと泣きを見そうな計算量なので、今回はExcelを使うことにしましょう。われわれは賢いアニマルなので。

ちなみに、1年が365日として同じ計算をしても、40人目の確率は10.9%（小数第2位を四捨五入）

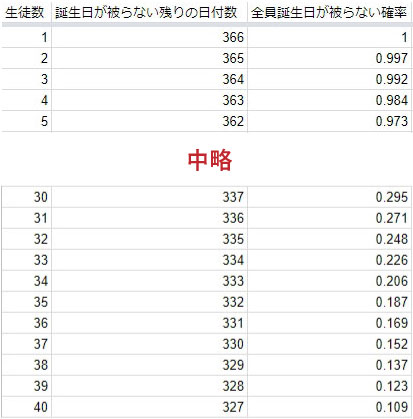
　A列に「生徒数」、B列に「誕生日が被らない残りの日付数」を入力して、C列にこれらを元にした計算結果「全員の誕生日が被らない確率（※）」を出力します。

※n人目の誕生日を選ぶ確率（A列/B列）に、n-1人目（1つ上のセル）の計算結果を掛けたもの

　すると、40人クラスで誕生日が同じ人がいない確率は0.109（10.9%）まで落ちることが分かります。したがって、4誕生日が同じ人がいる確率は、1-0.109=0.891（89.1%）。9割近い確率で、クラスの中に同じ誕生日の人がいることになります。

　というわけで、今回の結論。「1つのクラスに必ず同じ誕生日の人が1組以上いるという話は、数学的に考えると当たり前」。

　日本人の多くが10年以上学校に通い、小学校、中学校、高校と大きな生徒の入れ替えがあることを考えると、一度も誕生日被りを見ない人の方がよっぽどレアなはずです。

制作協力

QuizKnock