できることなら、もうけたい。
一夜にして、数千万〜数億円が手に入る可能性がある宝くじ。「そう簡単に当たるわけないんだよな」と落ち込んだり、「日頃の行いが良いからね」とゴキゲンになったりと、当選結果に一喜一憂した経験がある人は少なくないはずですが、実際のところ、“どれくらい当たる”ものなのでしょうか。
今回は、高校数学でも学習する「期待値」の考え方を使って「宝くじ1枚でいくら手に入るか」を考えてみます。
「期待値」とは?
そもそも「期待値」とは何なのかというと、「ある確率変数が平均してどのような値をとるか」を示す値であるといえます。ちょっと分かりにくいので、「サイコロの目の期待値」を例に挙げてみましょう。
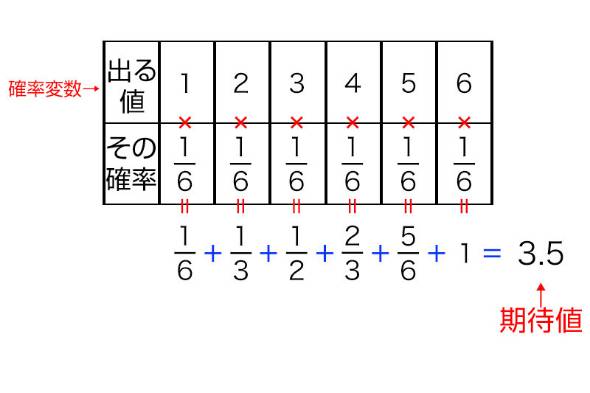
1から6まであるサイコロ面が、それぞれ同じ確率(=6分の1)で出るとします。出る目の値の平均は「1/6×1」「1/6×2」……「1/6×6」を全て足したもので、計算すると「3.5」になります。
サイコロの目のようなランダムに変化する値を「確率変数」と呼び、確率変数がとる値とそうなる確率の積を足し合わせていくと、得られる結果の平均、すなわち期待値が分かるというわけです。
定番! ジャンボ宝くじ
さて、ここからが本題。確率変数を「宝くじ1枚で得られる金額」として、その期待値を求めてみましょう。
まずは、定番とも言うべきジャンボ宝くじについて。
一般にいわれる「5大ジャンボ」とは、当せん金が高額な5つの宝くじの総称で、「バレンタインジャンボ(2月)」「ドリームジャンボ(5月)」「サマージャンボ(8月)」「ハロウィンジャンボ(10月)」「年末ジャンボ(12月)」を指します。
直近にあった2018年のサマージャンボでは、1等の5億円に当たる確率は0.00001%と微々たるものでしたが、6等300円まで行くと10%となかなかのものです。これらの「金額×確率」の値を足していったところ、期待値はおよそ141円でした。
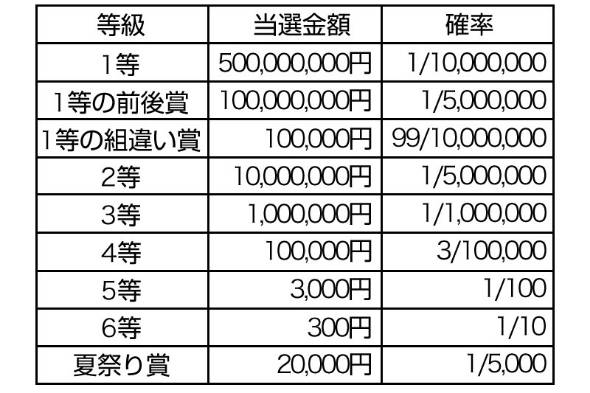
他のジャンボ宝くじや同時発売の「ジャンボ宝くじミニ(最高額が低め)」でも、おおむね同じ値が出ましたが、年末ジャンボはもう少し高く、昨年(2017)末で約150円の期待値。これらの宝くじは1枚あたり300円と価格が同じなので、狙うなら年末でしょうか。
スクラッチの場合
では、逆にチャンスが多いスクラッチではどうでしょうか。
スクラッチはいつでも販売されており、その場で当たり外れが分かるのが特徴です。回によってまちまちですが、今年(2018年)8月の「ドラゴンボールスクラッチ 魔人ブウ ラッキートライアル」は最高1000万円と、ジャンボ宝くじよりは低額ですが、その分当たりそうな気がします。
先ほど同様、各等の「金額×確率」を足して計算すると、「魔人ブウ ラッキートライアル」の期待値は90円となりました。1枚が200円のため、割合にすると45%。300円のものもありますが、どれも価格の45%程度の期待値であり、ジャンボ宝くじよりも低くなっています。
数字選択式宝くじの場合
続いては数字選択式宝くじを見てみましょう。この中には「ロト6」「ロト7」「ミニロト」や「ナンバーズ」「ビンゴ5」という、読んで字のごとく数字を選んで買う宝くじが含まれます。
同じくじなら価格は同じで、数字選択式宝くじの配当率は各等合計して45%と決まっており、期待値は原則どれを選んでも価格の45%です(実際には、100円未満が切り捨てられるので若干ブレますが)。
ジャンボ宝くじの期待値が150円(価格の50%)弱ということを考えると、「ジャンボ宝くじの方が良いんじゃ?」という結論になりそうですが……注目すべきはロト6、ロト7の「キャリーオーバー」という制度。
これは「1等の当たりが出なかった場合、次回にその分の金額を繰り越す」というもの。繰越金額は次の1等に上乗せされ、合計配当率45%とは“別に加算”されていきます。例えば、ロト7では1等の当せん金は最高10億円まで上がる可能性があるのですが、このときの各等の配当率の合計はおよそ58%になり、ジャンボ宝くじの期待値(の価格に対する割合)を上回ります。
まとめ
というわけで、「宝くじを1枚買ったときの期待値が最も高いのはキャリーオーバー時のロト6、ロト7で、次はジャンボ宝くじ」という試算の結果になりました。




<期待値で考える「宝くじ1枚でゲットできる金額」>
- ジャンボ宝くじ:購入額の約50%
- スクラッチ:約45%
- 数字選択式宝くじ:約45%
- 数字選択式宝くじ(キャリーオーバー時):約58%
※数字選択式宝くじ(キャリーオーバー時)は、ロト7最大時の場合
ただし、残念ながらというべきか当然というべきか、いずれも購入金額を上回る数値にはなりませんでした。「宝くじは夢を買うもの」ともいいますし、「一等当たっちゃったら、どうしようかな」とワクワクできるくらいの金額で購入するのが、楽しむコツなのかもしれません。
おまけ:数字選択式宝くじの仕組み
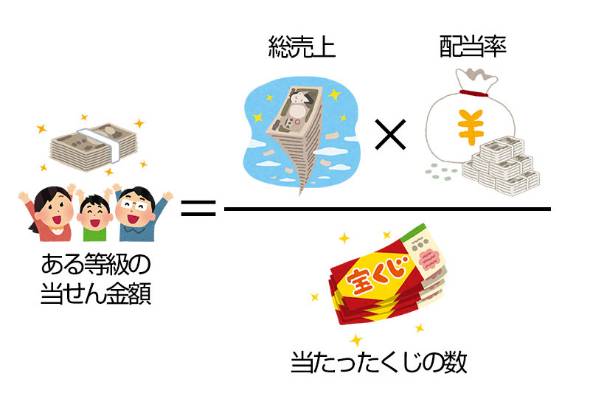
数字選択式宝くじは共通して、総売上の一定割合を決められた配当率に基づいて各等に割り振り、その金額を同じ等級の当たりくじに等分する「パリミュチュエル方式」という配当方式を採用しています。
ちょっと難しいのですが、この方式の期待値を算出する方法も紹介しましょう。
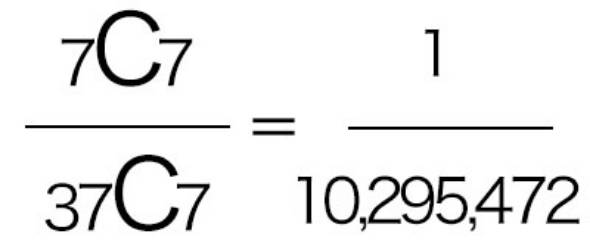
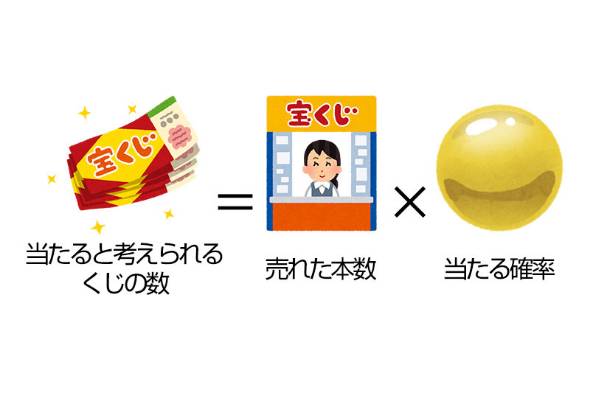
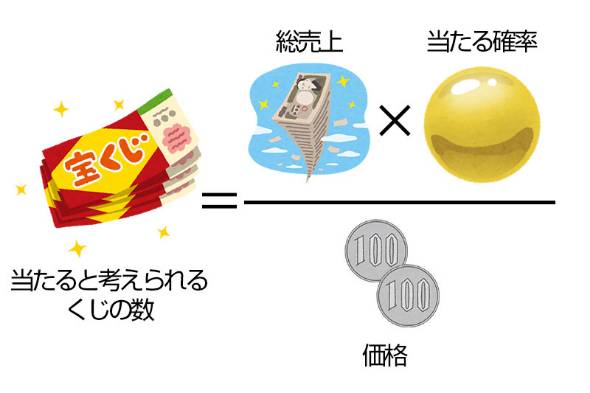
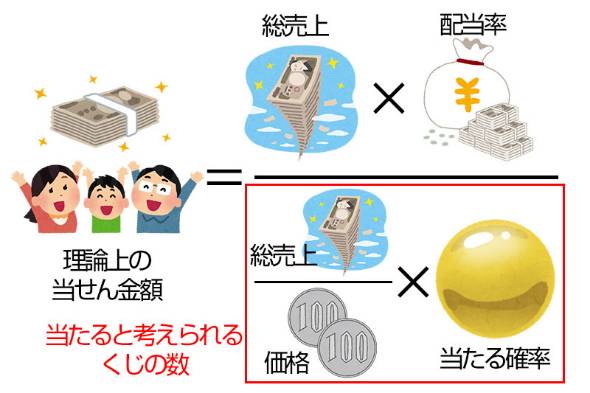
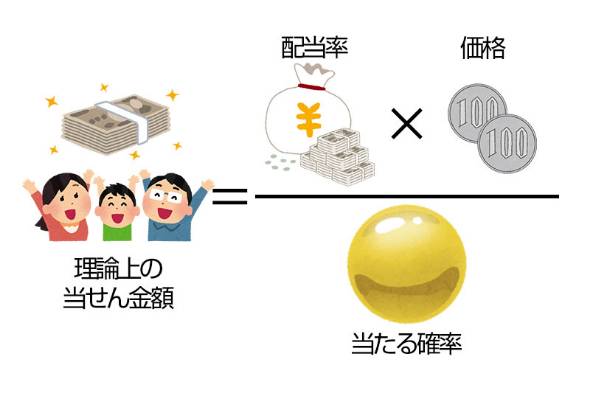


【修正】10月4日14時:一部画像の内容に誤りがあり、差し替えました。

