「入社したらイメージと違った……」なんて悲劇を起こさないためにも。
「求人情報と実際の条件が違った」「業務内容がイメージしていたものと違った」――こういった理由で、就職後に後悔する人は多いもの。本当に記載内容が実態と異なる場合もありますが、本人の確認不足などから募集内容を勘違いしていただけだったり、分かりにくい書き方にだまされていたりするケースもあります。
今回はそんなトラブルを回避するために知っておきたい「求人情報を正しく読むためのポイント」をご紹介します。

(1)給与条件は「理論年収」で比較しよう
キャリアカウンセリングで「年収に関して何か条件はありますか?」と質問すると、よく「賞与があった方が良い」「福利厚生が充実している方が良い」と返ってきます。しかし、このように給与条件の一部に着目していると、全体的な給与条件の良しあしを見誤ってしまうことがあります。
例えば、以下の2つの求人では、どちらの方が良い給与条件でしょうか?
<求人A>
- 月給:20万円(基本給16万円、業務手当4万円)
- 賞与:1.5カ月分(前年の平均支給月数)
- 福利厚生:住宅手当が2万円/月
- 平均残業代:3万円/月
<求人B>
- 月給:25万円
- 賞与:なし
- 福利厚生:なし
- 平均残業代:3万円/月
求人Aには賞与も福利厚生もありますが、求人Bにはありません。何となく見比べるだけだと、求人Aの方が良く見えるかもしれません。しかし、「理論年収」を割り出してみると、実際には求人Bの給与条件の方が良いことが分かります。
理論年収とは、月給に賞与、福利厚生の支給額を追加することで算出されるもので、より実態に近い年収が把握できます。
<理論年収の計算式>
理論年収=X×12カ月+(基本給×前年度の平均賞与支給月数)
※ X=月給(手取りではなく額面)+平均残業代+固定手当(住宅手当等)

求人A、Bに当てはめて計算してみると、実はBの方が年収が高いという結果に。このように理論年収は、複数の求人で給与条件を比較する際に役立ちます。
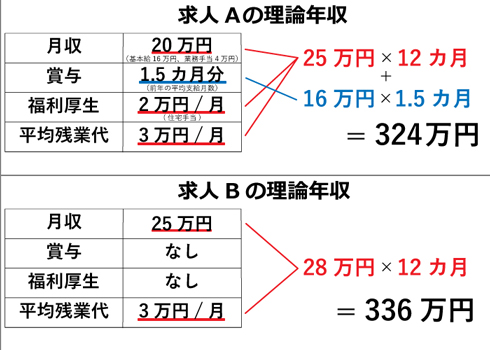
<求人A>
理論年収=25万円×12カ月+(16万円×1.5カ月)=324万円
※ X=20万円+3万円+2万円
<求人B>
理論年収=28万円×12カ月+(25万円×0カ月)=336万円
※ X=25万円+3万円+0円
また、もう1つ気を付けたいのは、賞与には「固定賞与」「決算賞与」があり、「決算賞与」は会社の業績が悪いと支給されない場合があるということ。例えば、Aの賞与が決算賞与だった場合、さらに給与条件が悪くなってしまうかもしれません。
(2)想定年収が、最高額でかさ増しされているかも
想定年収が記載されている場合は、それが平均額、最高額のどちらに基づいた“想定”なのかをチェックしましょう。
「入社3年目の想定年収が650万円」と書かれていても、これに該当するのは100人中1人だけで、平均的な想定年収は350万円……なんて場合もあります。
(3)実際の業務内容が異なる「募集ポジション詐欺」にご用心
膨大な求人情報の中から目当てのものを探そうと、募集ポジションの名称で検索。自然な行動ですが、実はここにも落とし穴があります。
というのも、企業側がより多くのエントリーを獲得するために、実際の業務との関連性が弱くても人気のあるポジション名を使っていることがあるからです。いくつか例を挙げてみましょう。
- 企画営業:実際の業務内容は敬遠されがちな新規開拓営業で、「企画」はいわば“釣り”
- コンサルティング営業:企画営業同様、「コンサル」という言葉で釣っていることがあります
- Webマーケティング:業務内容を詳しく見ると、数値管理が業務の大半なんてことがありがち
このような“募集ポジション詐欺”を回避するためにも、業務内容にもしっかり目を通しましょう。
UZUZ
UZUZは、第二新卒・既卒・フリーターといった20代に特化した就活サポートを行うベンチャー企業です。就活における「情報格差」「ミスマッチによる短期離職」をなくすために、就活サポートを実施しております。個別型サポートの「ウズキャリ」、研修型サポートの「ウズウズカレッジ」といったサービスを運営しています。


