勘だけで「センター試験全科目満点」を実現できる確率を計算してみたら、人生の大切なことが分かった

……べ、勉強しなくたって、できらぁ！（できるとは言っていない）

[QuizKnock，ねとらぼ]

　先日、東京大学の前期日程試験・第1次選抜の合格者が発表されました。これは2次試験の受験者を、センター試験の点数によって選抜するものです。

　その中では合格者の最高点・最低点・平均点が明らかにされているのですが……、な、な、なんとついに出てしまったのです。センター試験で満点を取った受験生が……！

第1段階選抜合格者の最高点・最低点及び平均点（東大Webサイトから）

お、俺たちだって運が良ければ満点とれる……ような気がするし！

　ご存じの通り、センター試験はマークシート式の試験。マークシートを埋めたことがある方なら、誰もが一度はこう考えたことがあるはずです。

　「この問題分かんないけど、テキトーに塗って当たらないかなあ……」

　理論上、可能性はあります。選択肢が4つだった場合、その問題に関しては4分の1の確率で当たることでしょう。分からなかった問題が4問あったならば、期待値で考えるとそのうち1問は当たるのです。

　……でも、本音はこうじゃありませんか？

　1問じゃ足りない。分からない問題を全部勘で当てたい。なるべく努力しないでセンター試験で満点が取りたい。

　「運も実力のうち」という格言もあるわけですし、どれくらいの確率で満点が取れるか、考えてみようじゃありませんか。

あなたがセンターで9割取れる受験生だとしましょう（仮定）

　今回は、実際に満点獲得者が出た「東京大学理科一類」に受かる見込みがある受験生を例に考えてみましょう。

　受験するのは先日満点が出た2018年度のセンター試験・本試。科目は国語・英語・数学IA・数学IIB・物理・化学・地理Bとします。国語と英語は200点満点、他は100点満点ですから、全科目で900点満点になります。

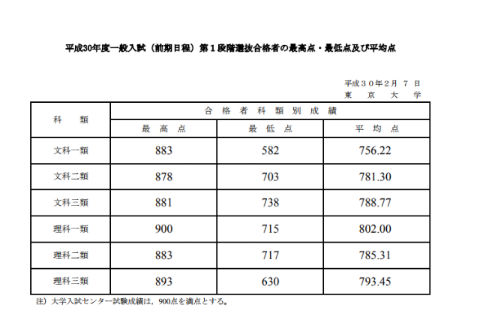
　理科一類に受かる見込みがある実力というと、具体的にはセンター試験で9割取れるレベル（第1次選抜合格者の平均点は802.00点なので、東大受験者の平均よりちょっと上程度です。

　話を簡単にするために、全教科でちょうど9割の点数が取れるとしましょう。あなたは残りの1割、つまり、90点分を勘だけでもぎ取る必要があります。

わずか90点だが……

国語（200点）

　全国平均が100点強のテストですから、180点も取れば十分な気もしますが、今目指しているのは満点の200点です。残りの20点分を何も考えずに強運だけでゲットして、友達に差をつけてやりましょう。

　「ちょうど9割正解できる実力（ここでは180点）」という前提通り、「第2問・問4」「第3問・問1（ウ）」「第4問・問4」の3つだけ解けなかったとしましょう。それぞれ配点は8点、5点、7点で、合計で20点になります。

　いずれも5択の問題なので、勘で全て当たる確率は1/5の3乗＝1/125。百分率に直すと0.8％です。ソシャゲのガチャなら「高額課金すればすぐに出る」くらいの数値でしょうか。残念ながらセンター試験ガチャは1年に1回しか引けません。でも、可能性がないわけではない、といったところですね。

英語（200点）

　国語同様、英語も180点までは確約されています。実際の受験生にとってはうらやましいことこの上ない話ですね。

　さて、残りの20点ですが、国語と比べて1問あたりの配点が低いため、5問必要となりました。

• 第1問B・問3（4択）
• 第2問A・問9（4択）
• 第4問B・問2（4択）
• 第6問A・問5（4択）
• 第2問C・問2（8択）

　勘で全て当たる確率は、1/4の4乗×1/8＝1/2048。百分率に直すとおよそ0.05％。国語と比べるとかなり厳しくなってしまいました。

数学IA（100点）

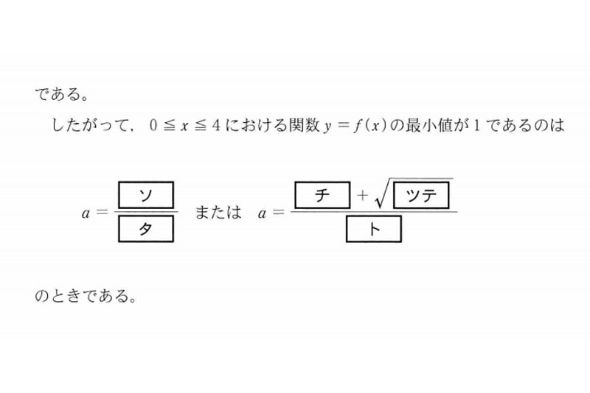
　このチャレンジにおいて、鬼門となるのが数学。なぜなら、解答となりうる選択肢が多すぎるのです。例えば、第1問の「ソ」「タ」ではある値の分子と分母が問われており、両方正解する必要があります。しかも、0〜9の10択です。

朝日新聞デジタルより

　わざわざ分数で表されているのだから「分母の『タ』は1ではない」「ソとタは互いに素のはず」など、問題が分からなくても推測できるポイントはありますが、全部無視します。だって、今回の目標は「勘だけで」正解することなのですから。

　ということで、この「ソ」「タ」を勘で正解できる確率は、1/10の2乗＝1/100。ちなみに、この問題の配点はたった2点です。

　さらに「第一問・チツテト」「第3問チツテ」「第4問セソ」を運良くというか、運だけで全問正解する確率は「1/100×1/10000×1/1000×1/100」で、1/100000000000（1千億分の1）となります。

---

　長いので、残りの科目はダイジェストで参ります。

数学IIB（100点）

　誤答：「第2問トナニヌ」「第3問ソタチ」「ナニヌネ」

　勘で全て当たる確率：1/10000×1/1000×1/10000＝1/100000000000（1千億分の1）

物理（100点）

　誤答：「第1問・問3」「第5問・問3」

　勘で全て当たる確率：1/8×1/8＝1/64（約1.5％）

化学（100点）

　誤答：「第2問・問3b」「第3問・問3」「第4問・問5b」

　勘で全て当たる確率：1/6×1/4×1/5＝1/120（約0.8％）

地理B（100点）

　誤答：「第2問・問4」「第3問・問5」「第5問・問5」「第6問・問2」

　勘で全て当たる確率：1/4×1/4×1/4×1/4＝1/256（約0.4％）

何回浪人したら「勘でセンター満点」ができるのか

　さて、各教科の確率が出そろいました。これらを全てかけて、センター試験満点の栄誉を勘だけで獲得できる確率を求めてみましょう。

　1/125×1/2048×1/100000000000×1/100000000000×1/64×1/120×1/256≒5×10の33乗分の1＝50溝（こう）分の1

　「東京大学理科一類に受かる見込みがある受験生が50溝浪すれば、なんとなく1回くらいはセンター試験で満点が取れそう」という結果になりましたが……こ、溝って何でしょうか。使い慣れない単位が出てきてしまいました。

　これがどのくらいの確率なのか例を挙げて説明してみましょう。

• 現在の地球上の人類70億人が、全員センター試験で9割取れるとする
• 人類誕生から現在までの日数（約1兆7000億日）かけて、2日に1セットずつセンター試験を解く

　この条件で満点が出る可能性は約1兆分の1。つまり、こんな感じのパラレルワールドが1兆個あれば、1回くらい満点が出てもおかしくありません。

　もう1つ例え話を。「地球上の全生物の中から、特定の1体を見つけ出す」という課題があったとしましょう。それはあなた自身かもしれませんし、上野にいるパンダや自室の布団に居るダニ、さっき飲みこんでしまった菌の可能性もあります。とにかくありとあらゆる生物の1体だけが当たりなのです。

　地球上には約30溝体の生物がいるそうなので、適当に提出した生物でクリアできる確率は30溝分の1。勘に頼って満点を取るのは、もしセンター試験で9割取れるまで頑張ったとしても、その1.7倍くらいシビアなのです。

　というわけで、今回の結論。「人生には、受験勉強より難しいことがある」。

満点を取りたいなら、たぶん勉強するのが一番早いと思います

制作協力

QuizKnock