隕石(いんせき)と同じ仕組みで燃やそうぜ!
皆さんは「火の玉ストレート」という言葉を聞いたことがありますか?
これは、藤川球児投手(阪神タイガース)が投げる、浮き上がるように見えるストレートの呼び名。うなるような豪速球でありながら、そのうえ、他の投手のストレートとは軌道が異なるという“魔球”っぷりを、火の玉という言葉で比ゆ的に表現しているのです。
でも、もしも本当に燃えて、文字通り「火の玉」になるストレートが投げられたら、どうでしょうか。
きっとどんなバッターでも、あまりの迫力に見逃し三振してしまうはず。高速で燃え上がる魔球は実現可能なのか、科学的に考えてみましょう。
断熱圧縮で原理を学ぶ
今回の目的である「火の玉ストレート(物理)」のように「速いスピードで空気中を移動し、炎上する」ものとして、よく知られているのは隕石(いんせき)です。

隕石が燃え上がるのには、空気との摩擦も影響していますが、それ以上に大きいのが「断熱圧縮」による効果です。
断熱圧縮というのは、空気を押しつぶしたときにその温度が上がる現象です。しかし、普通のピストンで空気を圧縮しても、ピストンの壁から熱が逃げてしまい、結果的に空気の温度は上がりません。断熱、すなわち、周りに熱を逃さないようにする必要があります。
隕石は猛スピードで空気に突っ込んでいるので、熱が逃げるよりも空気を押しつぶして温度が上がる効果が高いため、火の玉になるのです。その速度は、なんと時速数万キロから数十万キロ。温度も数万度に達し、隕石に含まれている鉄や岩石は真っ赤に融けて光ります。
革の発火点を考える
断熱圧縮を使って、野球ボールを燃え上がらせることはできるのでしょうか。野球ボールは革でできていて、その発火点はおよそ500度。絶対温度(※)に直せば773K(ケルビン)です。
※ 絶対温度とは、それ以下にできない最低温度(-273度)を0とした温度の基準。単位はK(ケルビン)。
つまり、ボールに触れている空気の温度を圧縮によって773Kまで上昇させればよい、ということになります。
隕石のような猛スピードのストレートが投げられる肩があれば話が早いのですが、そんなことは人間にはできません。今回のキーワードは「断熱圧縮」ですから、うまく断熱する方向で考えてみましょう。
ポアソンの法則を使う
ポアソンの法則によれば、周りに熱が逃げないようにした気体の温度と体積の間には「TV^γ-1=一定」という関係が成り立ちます。Tは絶対温度、Vは体積、γは比熱比と呼ばれるものです。今、空気はそのほとんどが窒素や酸素などの2原子分子でできているので、γ=1.4(※)となります。
※ 比熱比γは2原子分子理想気体の定圧比熱7/2と定積比熱5/2の比で7/5=1.4となる。
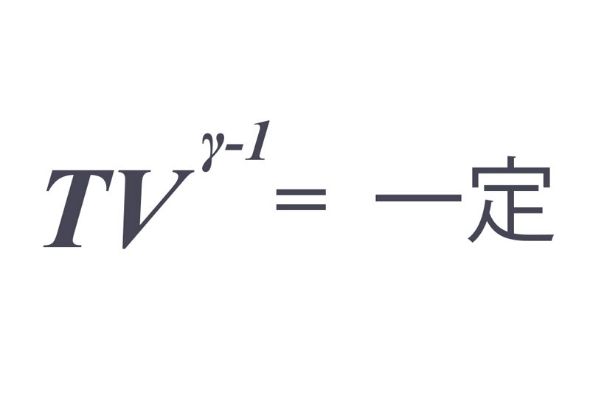
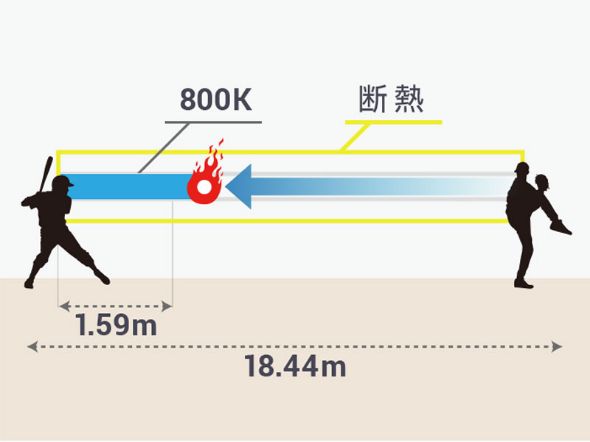
ボールの通り道だけに空気があり、その周りが真空(熱が伝わらない)、あるいは断熱材で覆ってある状況で投球したとしましょう。はじめは気温27度(300K)で、燃え上がるときはおよそ800Kになるとします。
ピッチャーからホームベースまでの18.44メートルのあいだの空気を押しつぶしていき、バッターから何メートルの地点でボールが燃えるか計算すると、1.59メートルになります。バッターの目の前まで来て、やっと燃え上がるわけです。意味あるのか、これ……。
止まる魔球
この方法には、もう1つ弱点があります。それは「空気を押しつぶしていくと空気の圧力も高まり、ボールが減速してしまうこと」です。
実は、先ほどの計算は外から力を加えてボールをいつまでも押し込んでよいという条件の下での計算。ボールを投げただけで空気の円柱を18.44メートルから1.59メートルまで圧縮しようとすると相当な速度が必要で、エネルギー保存則を使って計算してみたところ、時速563キロで投げる必要があることが分かりました。

というわけで今回の結論。「本当に火の玉になるストレートが投げられるなら、たぶん普通のストレートで十分」。


