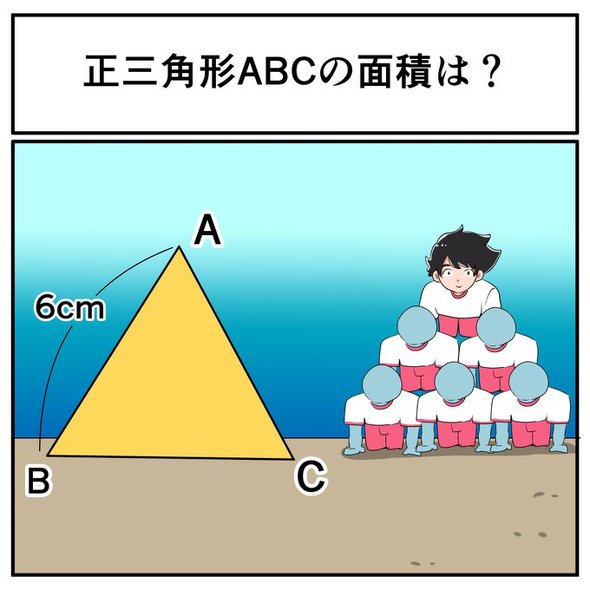
問題
答え
正解は「9√3平方センチ」でした!
【解説】正三角形の面積は1辺の長さが分かれば求めることが出来ます。というのは、正三角形の性質から、1辺の長さが分かれば他の辺の長さも分かりますし、角も全部60度だということが分かっているからですね。
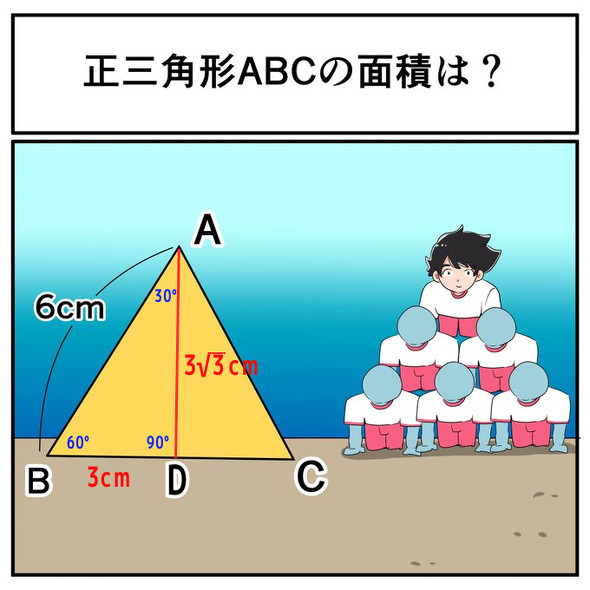
まずは頂点Aから辺BCに対して垂直に線を下ろします。その垂線と辺BCの交点をDとすると、三角形ABD・三角形ACDのどちらも“30度、60度、90度の直角三角形”になることが分かります。ちなみに、三角形ABDと三角形ACDは斜辺の長さが同じ(AB=AC=6センチ)で、ADが共通している直角三角形なので合同です。よって、「BD=CD=3センチ」となります。
続いて、辺BCに対する高さであるADの長さを求めたいので、直角三角形ABDについて三平方の定理を使うことにします。「AB=6センチ」「BD=3センチ」「AD>0(辺の長さなので)」から、計算は以下のようになります。
AD2+BD2=AB2
AD2+32=62
AD2+9=36
AD2=36−9
AD2=27
AD=√27=√32×3=3√3(AD>0より)
これで高さが「3√3センチ」だと分かったので、正三角形ABCの面積は「6×3√3÷2=9√3」平方センチになります。ちなみに、直角三角形の3辺の比は「BD:AB:AD=1:2:√3」となるわけですが、このことから“30度、60度、90度の直角三角形”の3辺の比が「1:2:√3」になるという有名な性質も導けます。
さらに、そこから1辺の長さがaの正三角形の高さは「(a/2)×√3」になることが分かるので、正三角形の面積を求める公式として「a×(a/2)×√3×(1/2)=(√3/4)a2」も導くことができたりします(「√3/4」は「4分のルート3」)。これを使うと、今回の問題も「(√3/4)×62=(√3/4)×36=9√3(平方センチ)」と一瞬で計算できたわけですね。
おすすめ記事
ねとらぼのクイズ記事
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
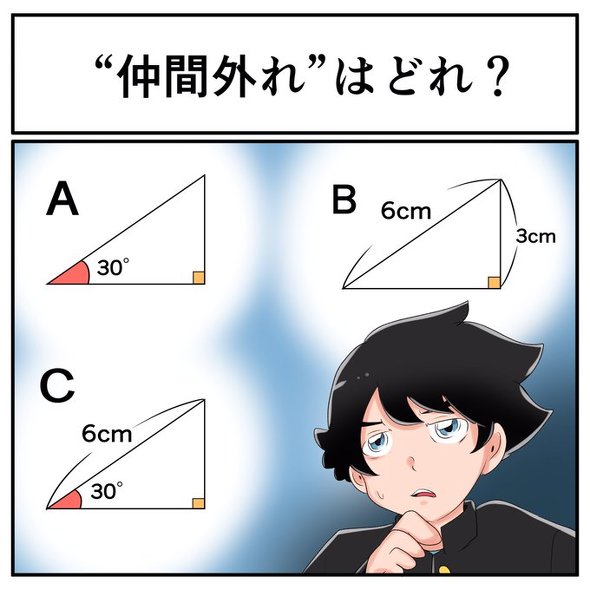
 この中に「仲間外れの三角形」が隠れています 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
この中に「仲間外れの三角形」が隠れています 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
大人になって解いてみると、意外と難しい。 三角形の内角の和はどうして180度なの? 中2なら秒で分かるかもしれないクイズ【数学・図形の性質】
三角形の内角の和はどうして180度なの? 中2なら秒で分かるかもしれないクイズ【数学・図形の性質】
大人になって解いてみると、意外と難しい。 121の平方根を求めよ 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
121の平方根を求めよ 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
大人になって解いてみると、意外と難しい。 「x^2+3x+2=0」を解け 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
「x^2+3x+2=0」を解け 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
大人になって解いてみると、意外と難しい。 2次関数のグラフのことをなんという? 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
2次関数のグラフのことをなんという? 中2なら秒で分かるかもしれないクイズ【番外編・中3数学】
大人になって解いてみると、意外と難しい。 「5a×6ab」を計算せよ 中2なら秒で分かるかもしれないクイズ【数学・式の計算編】
「5a×6ab」を計算せよ 中2なら秒で分かるかもしれないクイズ【数学・式の計算編】
大人になって解いてみると、意外と難しい。