“微分積分は何の役に立つのか”が分からない人向け文章問題作ってみた　「タカシ君のこたつが温まるのにかかる時間は？」

解説：もっと詳しく計算方法が知りたい人向け

　まずは問題文の最後にある「こたつの温度上昇率は、こたつの温度とヒーターの温度の差に比例するものとします」という一文をやっつけてしまいましょう。

　まず比例とはなんでしょう。細かい説明は省きますが、例えば「xとyが比例する」と言ったら、次のように書けるという意味です。

• y＝a×x

　この式は「xを何倍かするとyになる」という意味です。そしてこの「何倍か」が常に一定のとき、「xとyは比例する」と言います。「2倍」であればy＝2xですし、「3倍」であれば「y＝3x」になります。

　従って、最後の一文は次のように書けます。

• （温度上昇率）＝a×（こたつとヒーターの温度差）

　日本語で書かれていた文章が、なんだか数式っぽくなりました。でもまだ日本語がいっぱい入っていますね。これも全部数式にしてしまいましょう。

　「こたつとヒーターの温度差」は、引き算で求まります。ヒーターの温度は35℃でした。一方こたつの中の温度はちょっとずつ変わっていくので、Tで表すことにします。するとこれは「35−T」と書けますね。

　次に温度上昇率です。温度上昇率というのは「ある瞬間にどのくらい温度が上がるか」ということです。

　タカシ君は最初、10℃からこたつを温め始めました。この瞬間の温度上昇率はいくらでしょうか。上述の計算式に当てはめると

• a×（35−10）＝a×25［℃／時］

　であることが分かります。

　さらに温度が上がって15℃になると

• a×（35−15）＝a×20［℃／時］

　もっと温度が上がって、20度になると

• a×（35−20）＝a×15［℃／時］

　aの大きさは一定なので、温度が上がるほど温度上昇率は下がっていくことになります。つまり、最初は勢いよく温度が上がりますが、時間がたつと緩やかに上がっていくようになるのです。

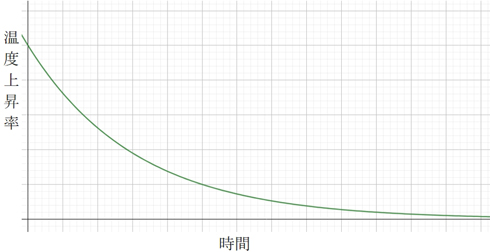
　このような場合、どうすれば温度上昇率を計算できるでしょうか。1時間で割ってもダメなことはさっき言った通りです。30分でもまだ長いです。1分でも1秒でも、0.1秒でも0.01秒でも、その間に温度上昇率は変わります。もっとずっと短い時間で割らないといけません。本当に一瞬の時間で割る必要があるのです。

　仕方がないので、その短い時間を「dt」と書くことにしましょう。そしてその間に上がった温度（こちらは小さいかもしれないし、大きいかもしれません）を「dT」と書くことにします。すると温度上昇率は、「dT/dt」と表すことができます。

　はい、これが「微分」です。微分とは、ものすごく小さい間（時間でも長さでも可）にどのくらい変化するかを表す計算なのです。これでようやく、問題文の最後の一文を数式で書けるようになりました。

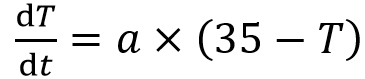
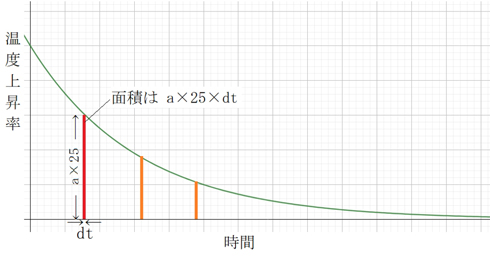
　対して、温度の上昇量は、グラフの下に細い長方形の面積として現れます。積分を使うと、グラフの下の面積を求めることができるのです。

　ここで使うのが積分。実際に計算すると「log」「e」といったややこしい話が出てきますが、「約1時間12分32秒」という答えが導き出せます。

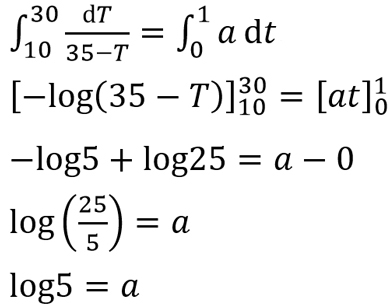
「（温度上昇率）＝a×（こたつとヒーターの温度差）」の「a」の値を求める式

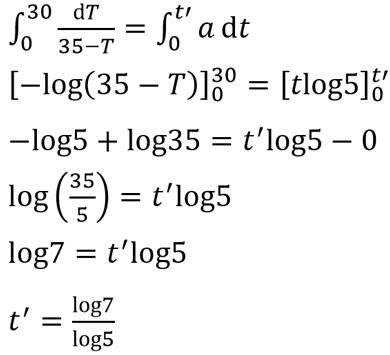
t'の値を電卓で計算すると、約1.209時間、すなわち約1時間12分32秒だと得られます。こたつがぬくぬくになるまでの時間が分かったね、やったー！

（キグロ）