【統計学で考える】都市伝説「しゃっくりを100回すると死ぬ」は何秒後に死ぬのか

詳細版：もっと詳しく知りたい人向け「統計学的に考えるしゃっくりの都市伝説」

　しゃっくりの間隔は、ランダムといえどおおよそ同じような長さです。平均10秒なら、5秒や15秒になることはあっても、1秒や30秒になることはほとんどありません。また、100回目に近づくほど間隔が短くなったり長くなったりすることもありません。そして、前回の間隔が長いと次の間隔が短くなる、といったこともなさそうです。

　このような現象は、「指数分布に従う」と推測されます。

　指数分布とは何でしょうか。これは、まさに上記のような「（以前の発生とは関係なく）平均して△秒の間隔で起こる現象が、次は何秒後に起こるかを表す確率分布」です。

　確率分布とは何でしょうか。これはちょっと説明が長くなります。

　「確率」と聞くと、「サイコロを振って1の目が出る確率」などを思い浮かぶ人が多いでしょう。1の目が出る確率は1／6です。2の目も、3の目も、同じく1／6で出ます。このことは次のように表で書くことができます。

　このように、出目（これを確率変数と呼びます）に対する確率を全て表現したものを確率分布と呼びます。

　特徴的な確率分布には、名前がついているものもあります。サイコロのように、全ての確率変数が等しい確率で出る分布は、「一様分布」と呼ばれます。指数分布も、このような確率分布の1つです。

　ところで、しゃっくりの発生間隔は「時間」です。これを1秒ごとに一覧にしたら巨大な表になってしまいます。かといって1分ごとでは正確な死亡時間が出せません。

　そこで、関数を使います。指数分布は、以下のような関数で表すことができます。

• f(x)=(1/λ)e^(-x/λ)

※正確には「指数分布の確率密度関数」と呼ばれるものです

　なにやら妙な記号が使われていますが、この関数は「平均λ秒の間隔で起こるしゃっくりが、x秒後に起こる確率」を表したもの。

f(x)=(1/λ)e^(-x/λ)

※正確には「指数分布の確率密度関数」と呼ばれるものです

• f（x）：確率分布を表すのによく使う記号で、「xになる確率はこれこれ」と述べるために使います
• e：自然対数の底と呼ばれる数で、約2.7182です。円周率のようなものだと思ってください
• λ（ラムダ）：「次に起こるまでの平均時間」を表します。今回の場合は10秒ですね。
• x：次にしゃっくりが起こるまでの時間

　でも、どうしてこんな関数で表されるのでしょうか。その詳しい説明は長くなるので省略しますが、なんとなくそれっぽい説明をしましょう。

　この関数をグラフにすると、次のようになります。

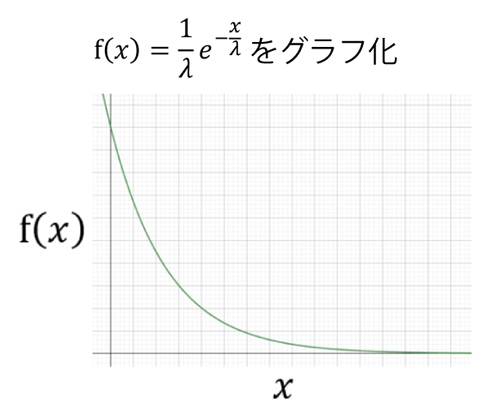
　横軸がxで、縦軸がf（x）です。xが小さい場合（間隔が短い場合）ほど確率が高く、大きい場合（間隔が長い場合）ほど低くなっていきます。

　なぜこうなるのでしょうか。例えば、30秒後に「次の」しゃっくりが起こるためには、0〜29秒までの間にしゃっくりが起こってはいけません。しかし、29秒もあったら、その間に1回くらいしゃっくりが起こってしまいそうです。

　一方、10秒後に「次の」しゃっくりが起こるためには、我慢すべき時間は0〜9秒までの9秒間です。このくらいなら、しゃっくりは起こらないこともあるでしょう。つまり、「△秒後に次のしゃっくりが起こる確率」は、「△秒後までしゃっくりが起こらない確率」に強く関係し、時間が長くなればなるほどこの確率は下がっていくのです。

　それをグラフで表現すると上のようになり、このグラフを数式で表すと「f(x)=(1/λ)e^(-x/λ)」となるのです。

　この説明は正確でも厳密でもありませんが、これを正確かつ厳密にして数式で書くと、この関数に辿り着きます。数学が得意な人は挑戦してみてください。

2019年9月26日14時35分　追記：計算式の一部に誤りがあったため、修正いたしました

（キグロ）