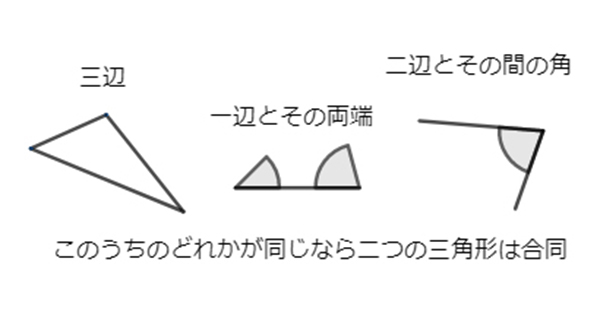
「二組の辺の長さとその間の角が……」って覚えてます?
INDEX
鉄骨は、基本的には伸び縮みしません(実際にはしますが、材料力学などの複雑な議論がしたいわけではないのでここでは無視します)。つまり、鉄骨で作った三角形は、三辺の長さが決まります。そして三角形は、三辺の長さが決まると、変形できなくなります。
従って、鉄骨で作った三角形は変形しません。それで建物を支えれば、崩れにくくなるのです。こんなところに、三角形の合同条件は利用されているんですね。
二組の辺の長さとその間の角が等しい
次は「二組の辺の長さとその間の角が等しい」ですね。どんな応用が考えられるでしょうか?
三辺のときと同様に、これもまた「二本の辺とその間の角が決まると、三角形の形まで決まる(つまり、変形できない)」と考えましょう。
これを利用しているのは、三脚や傘です。傘には六本とか八本の骨があります。骨は全て長さが決まっていますね? そして傘を開いたとき、隣同士の骨は、その間の角度が決まっています。骨の根元が固定されているためです。
二本の辺とその間の角が決まっているので、三角形の形が決まります。そのため、傘は毎回同じ大きさに開き、ピンと膜が張るのです。
一組の辺とその両端の角
最後は「一組の辺とその両端の角」ですね。これはこんな場面に使えます。
例えばここに一本の木が立っていて、あなたはこの木の高さを知りたいとします。木は高く、上まで巻尺を伸ばすわけにはいかなさそうです。どうしたらよいでしょう?

こんなときは、まず木とあなたの距離を測りましょう。そして、木のてっぺんを見上げたときの目線の角度も測ります。さらに、木は地面に垂直に生えていると考えられるので、このような図が描けるはずです。
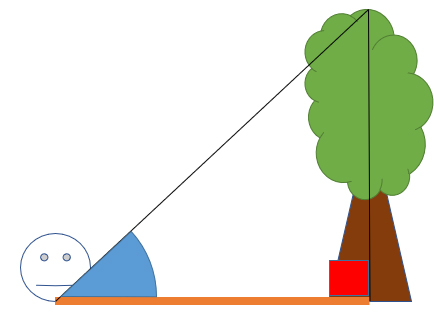
さて、この三角形の部分を抜き出してみましょう。自分、木の根元、木のてっぺんを頂点とする直角三角形ができますね。
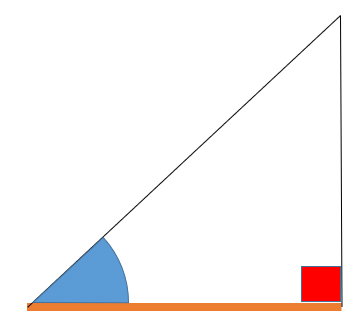
あなたはこの三角形について一辺の長さ(自分と木の距離)、その両端の角度(木を見上げる目線の角度、木と地面の角度/垂直)を知っています。
つまり、あなたはこれと全く同じ形の三角形を(地面などに)描くことができます。そうすれば、地面に描かれた三角形の一辺を測ることで、登らずに木の高さを知ることができるのです!
……もちろん、実際には木と同じ大きさの三角形を描くのは大変です。しかし数学には、その大変さを解消してくれる道具があります。説明は省きますが、「相似」とか「三角関数」とかがそれです。
ここでは木を使って説明しましたが、この方法はビルとか山とかにも使えます。それどころか、なんと星までの距離を測るのにも使われています。
三角形の合同条件はこんな風にちょっと見方を変えてあげると、いろいろと応用が効きます。テストで同じ形の三角形を選んでいるだけだとピンとこないかもしれませんが、実は意外とデキるやつなのです。