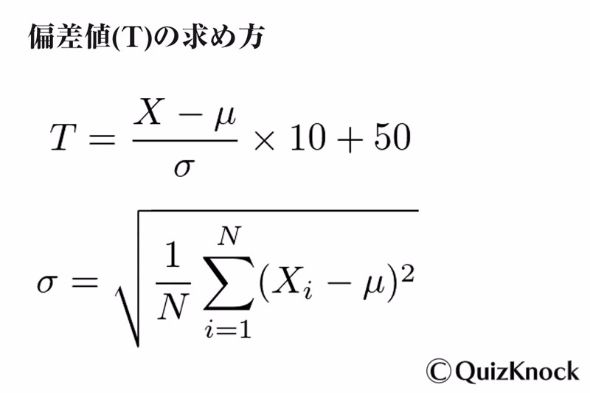偏差値とは結局なんなのか？

　来年受験を控える受験生各位については、そろそろ勉強に本腰が入り始めた頃だろうか。

　受験において重要な数字、偏差値。「やっべ前回より4下がった」とか、「B判定まであと3上げなきゃ～」とか、受験期は偏差値に一喜一憂させられたものである。

　そんな風に模試のたびに気にする偏差値だが、これが1上がったり下がったりすることにどんな意味があるのだろう？

偏差値とは

　偏差値の利用価値は、ずばり「比較可能である」ことにある。

　テストなどの得点のばらつき具合は、当然毎回違う。1000人のうち100位であっても、「101位以下をぶっちぎっての100位」なのか、「500位とほとんど点差のない100位」なのかでは、価値が変わってくる。

　そこで活躍するのが偏差値。偏差値を使うことによって、「自分が全体の真ん中からどれだけ離れた位置にいるか」を、別の回と比較可能な形で見ることができるのだ。

　つまり前述の例でいけば、順位は同じ100位であっても、前者（101位以下をぶっちぎった100位）のほうが後者より高い偏差値が出る。自分の実力アップが、偏差値なら簡単に比較して測れるのである。

偏差値の求め方

　より詳しく書くならば、偏差値Tは次の式で求められる（数学が苦手な人はここからしばらく読み飛ばしても可）。

　数式中のXは点数、μ（ミュー）は平均点を表す。σ（シグマ）は標準偏差と呼ばれる値で、受験者全員の点数から次のように求める。

　平方根を取る前のσ^2を「分散」と呼ぶが、分散や標準偏差が大きいほど平均点との差が大きい人が多いことになる。

　数式だけ見てもよく分からないので具体的に見てみよう。

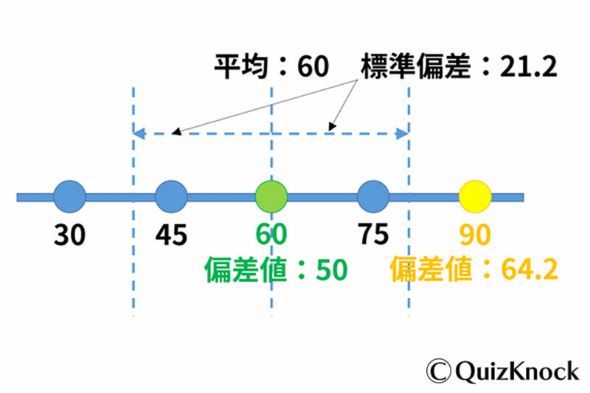
　5人でテストを行い、点数が高い方から順に90点、75点、60点、45点、30点だったとする。

　このとき、平均点は（90 + 75 + 60 + 45 + 30）÷ 5で、60点。

　分散は「平均点との差の2乗の平均」で、求めると（30 × 30 + 15 × 15 + 0 × 0 + （-15）×（-15） + （-30）×（-30））÷ 5で、450。

　標準偏差はこれの平方根をとって21.2となる。

　よって、90点を取った人の偏差値は（90 - 60）÷ 21.2 × 10 + 50で64.2。

　統計的な性質によって、よっぽどのことがなければ偏差値は0から100の間に収まるが、極端な得点分布をしたテストならば偏差値がマイナスになったり100を超えたりする。

　例えば、全世界74億人がテストを受けて1人が100点、73億9999万9999人が0点だったときの1人の偏差値は86万飛んで282。フリーザの戦闘力かよ。

偏差値を上げるには

　さて、本題に入ろう。偏差値を上げるにはどうすればいいのだ？

　一番順当に上げる方法は、もちろん自分の点数を上げることである。偏差値を求める数式から、偏差値を10上げるには標準偏差の値だけ点数を上げればよい。

　模試の結果には平均点などと一緒に標準偏差も載っているので、「何だこの数字？」などと無視せずに参考にしよう。

　さらに、偏差値を決める要素は自分の点数だけではない。平均や標準偏差をいじることができれば（※普通できないが）、偏差値も上がる。計算式から、成績の良い人のデータを除けば平均点と標準偏差が小さくなり、偏差値が上がることが分かる。

　つまり、成績がいい人がみんないなくなれば、勉強なんかしなくても偏差値は上がるのだ！　早速シミュレーションしてみよう。

　画像のような得点分布をした100人で考える。平均点は60.47点、標準偏差は10.43。

　70点を取った人の偏差値は59.1だ。

　さて、この分布から71点以上の人を消してみる。消された人は計16人。

　すると、平均点が57.52点、標準偏差が8.36にそれぞれ下がり、この状態で偏差値を計算すると64.9。

　偏差値が約60の人がいて、自分より点数の高い人が全員消えたとすると、偏差値の増加は5.8ポイント。10上げるって大変だ……。

　それもそのはず。偏差値70というのは、得点が正規分布に従っているときに上位2.3％以上の人が取る値である。偏差値60なら上位16％以上。

　仮に上位から（自分以外の）人が消えていったとき、自分が上位2.3％にくるためには、ざっと計算して上から14％ほどの人がいなくならないといけない。

　しかも、同じ「上位2.3％」でも、「山の裾近くの2.3％」と「山の裾を大きく削って作った2.3％」ではライバルの数が違うので、現実には消えてもらわねばならない割合はもっと大きくなる。

　試しにシミュレーションとして自分以外の上位30人が消えたとしても偏差値は70に乗るかどうか。

　同じことを10万人が受ける模試でやろうとすれば、消えてほしい人は3万人。フリーザ並みの戦闘力を持っていない限り、3万人に消えてもらう（？）より勉強した方が早そうだ。

まとめ

　偏差値を10上げるには、「今より標準偏差の分だけ良い点を取る」か、「受験者の上位3割に消えてもらう」。

　良い子の皆は後者を選んじゃダメだぞ。