黒い部分の面積を求めよ　中2なら秒で分かるかもしれないクイズ【番外編・中3数学】

答え

　正解は「24π−18√3」でした！

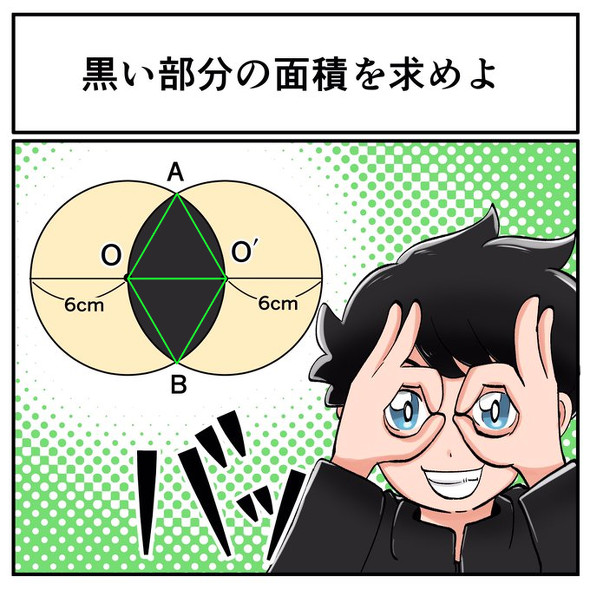
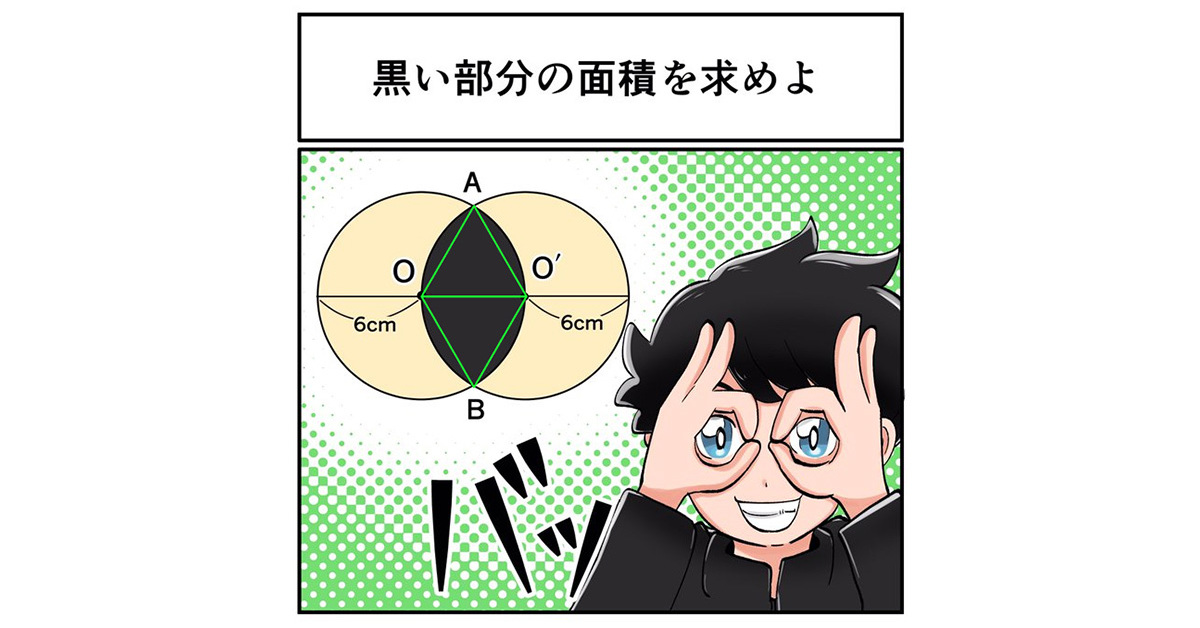
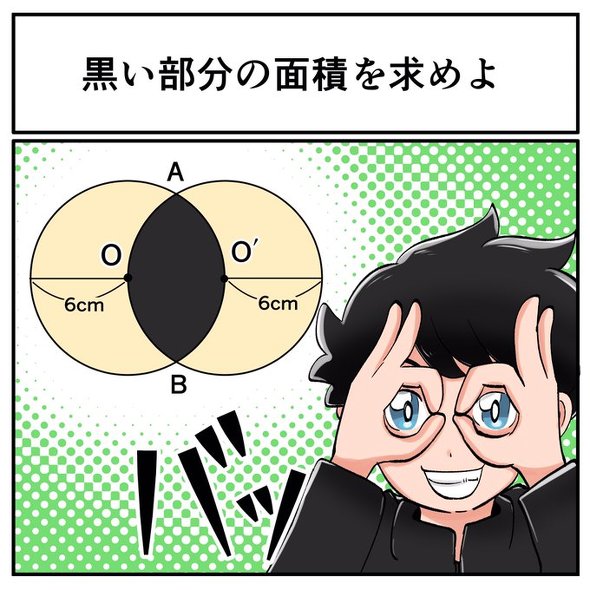
【解説】点OとO'は半径6センチの円の中心なので、「OO'＝6センチ」であり、点A、Bは2円の円周上の点であることから、「AO＝AO'＝BO＝BO'＝6センチ」となります。よって、△AOO'と△BOO'はどちらも1辺が6センチの正三角形だと分かります。

　さて、求める面積ですが、黒い部分はOO'を軸にして上下で線対称なので、上の部分を2倍すればよさそうです。また、上の部分はおうぎ形AOO'とおうぎ形AO'Oという2つのおうぎ形が重なった図形です。そして、その重複部分はちょうど正三角形AOO'1個分となります。

　したがって、上の部分の面積は「（おうぎ形AOO'の面積）×2−（正三角形AOO'の面積）」で求められ、黒い部分全体の面積は、さらにその2倍となります。

　△AOO'が正三角形であることから、おうぎ形AOO'の中心核は60度です。よって、おうぎ形AOO'、△AOO'の面積は以下の通りになります（正三角形の面積については関連記事を参照）。

• おうぎ形AOO'の面積＝6×6×π×（60/360）＝6π（平方センチ）
• 正三角形AOO'の面積＝（√3/4）×6²＝9√3（平方センチ）

　以上より、求める面積は「（6π×2−9√3）×2＝24π−18√3」平方センチです。

おすすめのクイズ記事