【数式で見ると分かる】“蛇口から出る水、下に行くほど細くなる現象”の理由

水が減っているわけではないのに、なぜ細くなる？

[キグロ，ねとらぼ]

　私たちの身の回りには、数式がたくさん潜んでいます。このシリーズでは身近に潜む数式の中から、筆者がお気に入りのものをいくつかピックアップして紹介していきます。

　蛇口からチョロチョロと水を出すと、その水は下に行くほど細くなっていきます。考えてみると不思議です。細くなるということは、水が減っているのでしょうか？　そんなことがあるのでしょうか？

水が透明なのでちょっと見にくいですが、下に行くほど細くなっています

ライター：キグロ

5分間で数学を語るイベント「日曜数学会」や数学好きが集まる部室みたいなもの「数学デー」の主催者。数学の記事を書いたり、小説『QK部』を書いたりしている。

“蛇口から出る水、下に行くほど細くなる現象”の数式

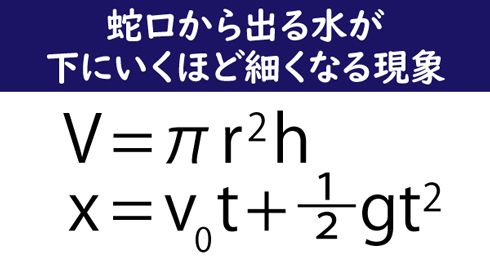
　その理由を説明するのが、こちらの2つの数式。

　1つ目は円柱の体積の公式。算数でおなじみですね。円柱とは、電信柱や竹のような円形の柱。この公式は、その体積が円の半径（r）と高さ（h）で決まることを教えてくれます。

　2つ目は落体の距離の公式。真下に投げた物体が、何秒後に何メートル落下しているかを計算できます。

　式の中の「x」は落下距離、「t」は時間。この式を使うと、時間（t）が増えれば増えるほど、落下距離（x）の“増え方”が増えることを教えてくれます。要するに「落とした直後（0秒後）〜1秒後の落下距離」よりも「1〜2秒後の落下距離」の方が大きくなるということです。

　さらに言うと「2〜3秒後の落下距離」の方が大きく、それよりも「3〜4秒後」の方が大きく……時間がたつほど落下速度が上がって、落下する距離が伸びていくイメージですね。

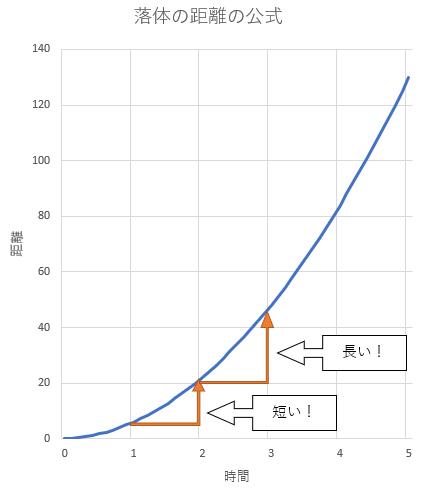
1〜2秒の間に落ちる距離より、2〜3秒のあいだに落ちる距離の方が長い

ポイントは「時間がたつほど、落下距離の増え方が大きくなること」

　仮に、蛇口をパッと開けて、1秒後にパッと閉めたとしましょう。このとき、「蛇口を開けた瞬間に出た水A」と、「蛇口を閉める寸前に出た水B」の動きを考えてみます。

　蛇口を開けた瞬間、水Aの落下距離は0です。一方、水Bはまだ出口にすら着いていません。1秒後、蛇口を閉めます。この瞬間、水Aはすでに1秒間落下していますが、水Bはようやく出口に着いたところです。

　ここからが重要です。

　水Aと水Bのあいだの距離は、1秒分の差があります（マラソンで選手間の距離を秒数で表すような表現をしています）。

　そして、落下距離の“増え方”は時間がたてばたつほど大きくなるのでした。水Aの落下距離の増え方が、水Bの増え方より1秒分大きいのです。そのため、“1秒分の差”はどんどん開いていきます。

　分かりにくい方は、100メートル走をイメージしてみてください。スタートを切った直後の選手たちはそこまで速くありませんが、走りながら加速していきます。ある選手がスタートに大失敗して、1秒遅れで走り出したとしましょう。スタートが遅れると、他の選手たちと同じように加速しても同じ速さになれません。そのため、他の選手たちの背中はどんどん遠くなっていくはずです。

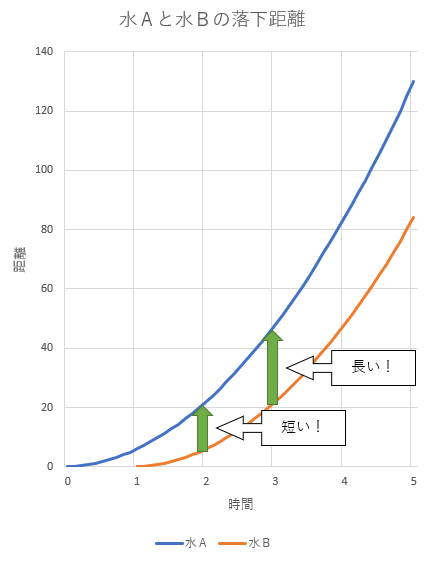
時間がたつほど、水AとBの差は開いていく

　さて、蛇口から出た水は、円柱のような形をしていますよね。水AとBの差は開いていくので、“水の円柱”の高さは伸びていきます。

　しかし、水全体の量（体積）は変わらないはずです。ということは……？

　円柱の体積は半径と高さで決まるわけですから、半径が小さくなるしかありません。だから、蛇口から出た水は徐々に細くなっていくのです――　最初に出た水と後から出た水の距離が、時間がたつにつれどんどん開いていくのだから。

（キグロ）