【数学のアレ、何に役立つ？】三角形の合同条件、「同じ形の三角形を見つけて、テストで5点くらいもらう」以外の使い方（1/2 ページ）

「二組の辺の長さとその間の角が……」って覚えてます？

[キグロ，ねとらぼ]

　物事にはたいてい、複数の見方があります。ある側面から見ただけでは気付けないことも、他の方向から見てみれば当たり前のように思えたりします。

　この記事では、そんなものの見方を1つご紹介しましょう。きっと誰もが知っている、「三角形の合同条件」のある側面についてです。

ライター：キグロ

5分間で数学を語るイベント「日曜数学会」や数学好きが集まる部室みたいなもの「数学デー」の主催者。数学の記事を書いたり、カクヨムで小説を書いたりしている。

中学校で学んだ「三角形の合同条件」、何の役に立つのか

　三角形の合同条件、覚えていらっしゃるでしょうか。きっと中学のときに、こんな問題に取り組んだはずです。

次の三角形のうち、合同な組を全て答えなさい

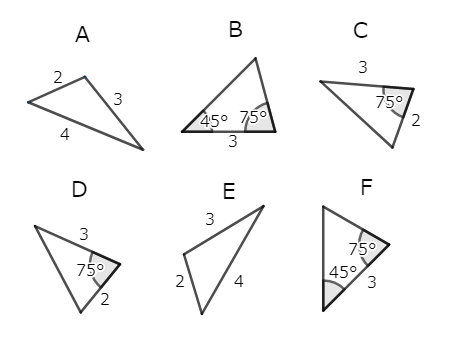
　なんとなく思い出してきましたか？　「全く同じ形の三角形を選ぶ」という、人生において役に立つか微妙な技を身に付けたのが、このときだったはずです。

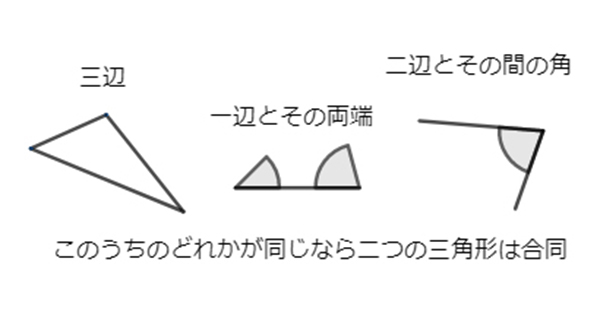
　三角形の合同条件は、次の三つです。

• 三組の辺の長さがそれぞれ等しい（先の問題でいうとAとE）
• 二組の辺の長さとその間の角がそれぞれ等しい（CとD）
• 一組の辺の長さとその両端の角がそれぞれ等しい（BとF）

　2つの三角形の間に、これらのうちのどれかが成立していれば、2つの三角形は全く同じ形（合同）だと言えるのでした。要は「三辺」「二辺とその間の角」「一辺とその両端の角」のどれかが分かれば、合同かどうか分かるわけですね。

　さて、この知識、いったい何の役に立つのでしょう？

　もちろん、二つの三角形が合同かどうか知りたいときに、役立ちます。でも、そんな場面、まずありません。どうしてこんなものを学ぶのでしょうか。

三組の辺がそれぞれ等しければ合同

　実は、三角形の合同条件は、ちゃんと役に立つのです。いったい、どういう場面で役に立つのでしょう？

　まずは「三組の辺がそれぞれ等しければ合同」について考えてみましょう。こんな場面を想像してください。

　例えばあなたが、長さが3センチ、4センチ、5センチの3本の木の棒を渡されたとします。これらを使って三角形を作ると、どう頑張っても同じ三角形しか作れません。なぜなら、あなたが作る三角形は、どれも三組の辺がそれぞれ等しいからです。

　そしてあなたの隣の人も同じ木の棒を渡され、三角形を作った場合、やっぱりあなたが作ったのと全く同じ三角形を作ります。なぜなら、それしか作れないからです。

　これは、「三辺の長さが決まると、三角形の形まで決まる」、つまり「変形できない」ということを意味します。

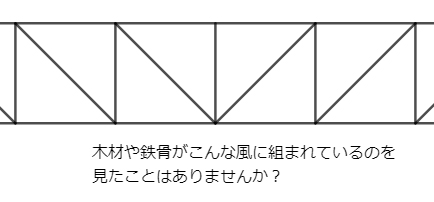
　だからなんだ、という感じもしますが、実はこれを利用して丈夫な建物をつくる技術があるのです！

　橋とかドームの天井とかで、鉄骨が三角形に組まれているのを見たことはありませんか？　このような構造を「トラス構造」と呼びます。