割り算とどっちが早いのだろう……

ある数が割り切れるかどうか、つまりnの倍数であるかどうかを知りたい場面は結構たくさんある。分数を約分するときや、身近なところだと割り勘を計算するときなどだ。
場面の多さに比して、ふつう倍数の判定は難しい。例えば「64811は11の倍数か?」に瞬時に答えられる人はそう多くないはずだ。
ただし、いくつかの小さい整数に対しては、その倍数に関する法則が広く知られていて簡単に見分けられることがある。
例えば、2の倍数なら必ず一の位は2の倍数(偶数)になる。3の倍数であれば、各桁の数字を足し合わせると和が3の倍数になる(例:357→3+5+7=15は3の倍数)。特に3の倍数の判定法は簡単なので知っておくと便利だ。
ほかのいくつかの素数に対しても、簡単な判定法があるので以下の画像にまとめてみた。また、合成数の判定はこれらを組み合わせて行えばよい(例えば6の倍数は2と3どちらの倍数でもあることを判定することと同じ)。
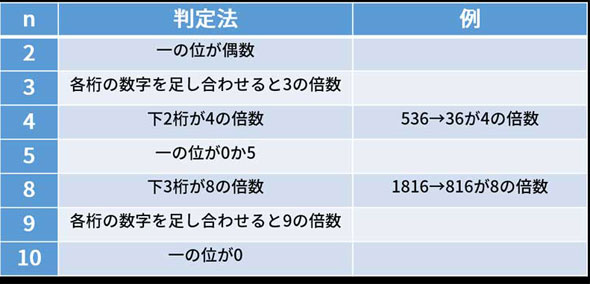
ここに挙げたような例は覚えやすいし楽な判定法であり、一般によく知られている。ところが、7や11の倍数の判定法はあまり耳にしない。
調べてみると、7の倍数ならこんな方法が出てくる。
数を3桁ごとに区切り、位が小さい方から引く→足す→引く→……を繰り返すと結果が7の倍数になる
(例:4534845→-845+534-4=-315で7の倍数、よって4534845は7の倍数)
うーん、ややこしい! 3桁ごとに区切って足し引きするのがもう大変だし、結局3桁の数を7で割ってみないと分からない。
11の倍数も13の倍数もこんな感じの役に立たなそうな方法が出てくる。もう少しシンプルにならないのか。
万能の判定法、現る
上の7の倍数の方法がなぜイヤかというと、「何桁で区切るんだっけ?」「どの順番で足すんだっけ? 引くんだっけ?」が覚えられないからだ。覚えてもこの方法は基本的に7の倍数にしか使えない(※)し、もう面倒くさいから割り算しちゃえと思ってしまう。
※この方法は1001=7×11×13であることに基づく方法なので、11と13の倍数には使うことができる
そこで調べてみると、どんな数の倍数でも同じような手順で判定できる方法があるらしい。なんだ、それを最初から教えてくれればいいのに。
その方法とはズバリこれ。
「一の位の数字に2をかけて、1の位を切り落とした残りから引く」→「nの倍数かどうかを見たい時、nで割って割り切れるかを見る」
ナンノコッチャなので、具体例を。例の7の倍数でやってみたい。ある数が7の倍数なら、「一の位の数に2をかけて、残った数から引いても7の倍数」。例えば294なら、一の位の4に2をかけた8を29から引くと21。これは7の倍数なので、294は7の倍数である。先ほどの方法では3桁の数字は割るしかなかったが、この方法なら簡単に判定できる。
さっきの4534845とかいうでかい数でも、4534845→453474→45339→4515→441→42と、同じ操作を繰り返せば7の倍数が判定できる。さっきの3桁区切りよりもだいぶ楽だ。
仕組みはこうだ
さて、どうしてこのようになるかを説明する。「ある数」が、0〜9の整数aと任意の自然数Aから「10A+a」と表せるとする。このとき、一の位の数に2をかけて、残った数から引いた結果は「A-2a」となる。
「ある数」10A+aが7の倍数ならば、等式7k=10A+a(kは自然数)が成立して、aについて解くとa=7k-10A。これをA-2aに代入して整理すると21A-14kとなり、14kも21Aも7で割り切れるから、A-2aは7で割り切れる。
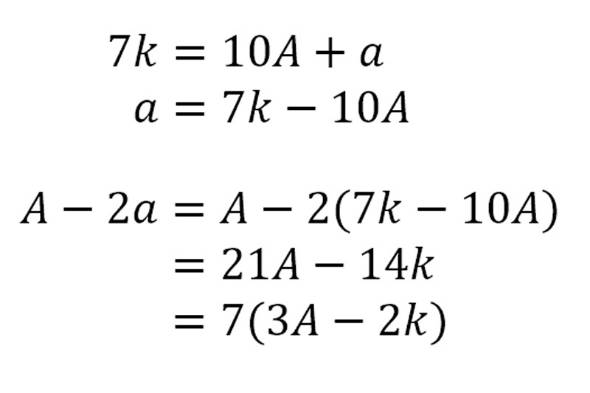
ここからが本題。この説明の7をp、「一の位にかける数2」をnに置き換えれば、あらゆる数の倍数の求め方が見えてくる。
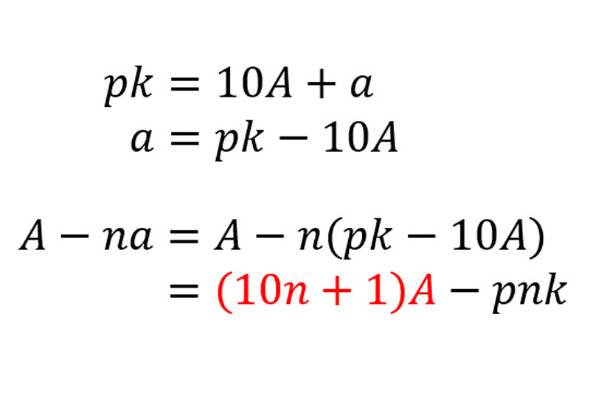
10n+1(赤字の部分)がpで割り切れれば、A-naはpで割り切れる。従ってnをpに応じて定めることで、どんなpでも同じ方法で倍数判定が行えるというわけだ。そんなnを見つけるのは一見大変そうだが、10n+1の一の位はnが正ならば1、負ならば9になることに着目すればそれほど難しくない。
例えばp=37なら、一の位を1にするなら3倍(37×3=111)、9にするなら7倍(37×7=259)。10n+1を111にするならn=11、-259とするならn=-26とすればよい。
なお、nを負とするなら、「一の位に負の数をかけて引く」ので結局足し算をすることに注意が必要だ。
まとめ
ここまでを整理すると、ある数がpの倍数かどうかを見分けるには次のようにすればいいことが分かる。
- 10n+1がpで割り切れるようなnを見つける
- ある数の一の位のn倍を、十の位より上の数から引く
- 結果がpの倍数かどうか分かれば終了、分からなければ再び2を行う
方法さえ覚えておけばnを決めるだけで使えるのがうれしいポイント。
参考までに、代表的な素数pに対するnの例を示しておく。p=3はn=-1で成り立つが、これは冒頭で挙げた「全ての桁を足し合わせる」と同じことになる。
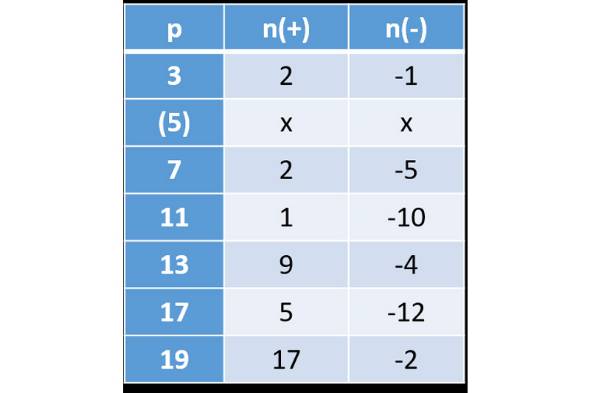
nの絶対値が大きいと割り算と同じくらいしんどいが、特に19の倍数などは2をかけて足すだけなので使えそうだ。12065は、12065→1216→133→19で、19の倍数!
7の倍数とか13の倍数とか分かりにくいわ! とずっと思ってきたが、これで全て解決!
……と言いたいところだが、割り算するのとどちらが早いかといわれると微妙なところではある。ただし汎用性はある方法なので、覚えておいて損はないと思う。

