話題の入試問題「じゃんけんに新たな手『キュー』を加えて別のゲームを作りなさい」 東大生の答えは？

実際に入試で出くわしたら頭を抱える。

[QuizKnock，ねとらぼ]

　今年、ある「ユニークな大学入試問題」がネット上などで注目を集めたのをご存じだろうか。

じゃんけんの選択肢「グー」「チョキ」「パー」に、「キュー」という選択肢も加えた新しいゲームを考案しなさい。解答は、新ゲームの目的およびルールを説明するとともに、その新ゲームの魅力あるいは難点も含めて、601字以上1000字以内で論じなさい。

（2018年度・早稲田大学スポーツ科学部　小論文入試問題）

　勝ち負けを決めるゲームの中で最もシンプルかつ、最も一般的なものといえる「じゃんけん」。完成されたこのゲームに自分なりの独自ルールを加え、新たなゲームとせよ、という問題だ。

　どんな答えを書けばいいのか、思わず頭を抱えてしまいそうだが、この問題に3人の東大生がプレゼン形式で挑戦したので内容を紹介しよう。

プレゼン1：順位を決められるじゃんけん

　まずは1つ目の案から。

　この案では新しい手「キュー」を、既存の手「グー・チョキ・パー」と同じような4つ目の手として扱い、それぞれに対する強弱を決める（画像参照）。

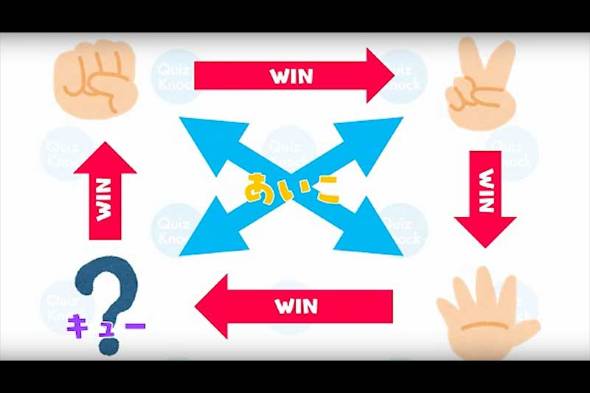
　このルールでは、一般的なグーとパーの間にキューが入り、グーはチョキに、チョキはパーに、パーはキューに、キューはグーに勝つ。また、グーとパー、チョキとキューはともにあいことなる。

　このルールのメリットは、3人以上で戦った場合に「順位が決まる」ということだ。つまり、3人でやったときに、一発で「2位」を決められる（ことがある）という点。

　例えば、3人の手がそれぞれ「グー」「チョキ」「パー」だった場合、通常のじゃんけんのようにあいこにはならずに、「グーの人：1勝1分」「チョキの人：1勝1敗」「パーの人：1分1敗」となる。

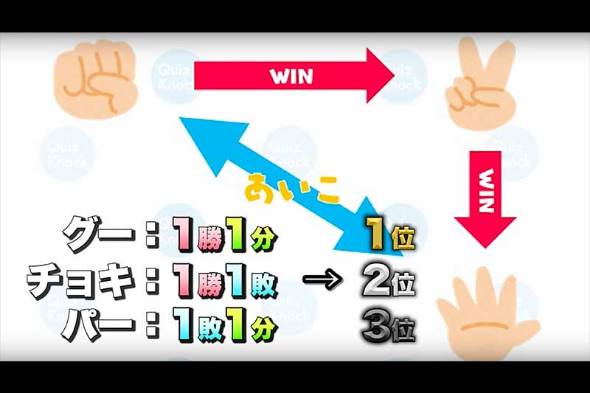
　勝ち＞あいこ＞負けの順に得点が高いと考えれば、1位：グー、2位：チョキ、3位：パーとなる。順番決めのじゃんけんなどで役に立つルールと言えそうだ。

プレゼン2：1対大人数でのじゃんけん

　続いて2つ目の案。

　もとの問題文には「新ゲームの目的」を説明せよ、とあるが、この案はかなり特殊な状況を想定している。それは「1人対多数のじゃんけん専用ルール」だということ。

　パーティーなどの大人数の場で、プレゼントなどをもらえる数人を選出したいとき、「司会者対その他大勢の人」という形式でじゃんけんをすることがあるだろう。

　この案では、キューの手を使えるのは「司会者」に当たる1人だけ。この人は、右手では大勢を相手に普通の手を出すが、左手は隠しながら「キュー」か「キューなし」か、どちらかの手を選んで出しておく。

　つまり、司会者の出す手は（グー、チョキ、パー）×（キューあり、キューなし）の6パターンとなる。

　司会者は、まずは右手で手を出し、その後に隠していた左手を出して「キューがあるか、ないか」を見せる。

　勝敗は、左手がキューの場合は「あいこの人が脱落（つまり負け）」、左手がキューでなかった場合は「負けの人が脱落（通常通り）」というルールだ。

　このルールによるメリットは、「キューがあるか、ないか」という緊張感で、じゃんけんが2度楽しめるという点。右手のじゃんけんで負けていた場合でも、左手がキューであれば先に残れる。つまり、“敗者復活”のようにもう一度ドキドキを楽しめるのである。

　また、左手は隠されているので、考えようによっては「後から改変可能な手」でもある。これを司会者がズルく使えば、司会者には「残したい子を必ず残せる」というメリット（？）があるし、逆に参加者には「司会者に嫌われていると負けやすくなる」というデメリットがあるとも言えるだろう。

プレゼン3：勝率が同程度になる平等なじゃんけん

　最後の案は、「キュー以外の（キューを除いた）手があいこだった場合は、キューが勝ちになる」というルール。これは4人以上でじゃんけんをすることを想定している。

　4人でじゃんけんをして、「グー、チョキ、パー、キュー」となった場合は、その他の手があいこなので「キュー」の勝ち。同じように「グー、グー、グー、キュー」でも「キュー」の勝ちである。

　「グー、チョキ、キュー、キュー」など、キュー以外の手で勝敗がついている場合は通常の勝者（この場合はグー）が勝ちとなり、キューは負けたことになる。また、「キュー、キュー、キュー、グー」のようにキューが多数となった場合は、他の手を出した1人の勝ちとする。

　4人でじゃんけんをした場合のそれぞれの手の勝率は大体20%程度で等しい。

　このルールのメリットは、「キューの存在で、あいこの可能性がかなり低くなる」ということ。これにより、ゲームをスムーズに進行できる。

本当に平等なのか計算してみた

　4人では勝率が20%程度と等しく感じられたが、実際に計算してみると不公平極まりないルールであることが分かった。特に7人以上のじゃんけんではキューを出せば50％以上の確率で勝ててしまう。キュー以外の手の勝率は6人以上で25%未満となり、グーやチョキを出す理由がなかった。

　ゲームとして成り立たないのでは……。

楽しければ良い

　いろいろなルールを紹介したので、興味がある方はぜひやってみてほしい。また、「キュー」を加えたこれ以外の新ルールも考えると楽しいはず。

東大生がこれらを真剣にプレゼンする動画

制作協力

QuizKnock