数秒で解ける？ 名門・慶應義塾中等部の入試問題で小学生と勝負！
これが解ければ慶應ボーイ・慶應ガールになれる……かも？
有名な中学校の入試問題は、「これ本当に小学生が解くの？」と驚いてしまう難問ぞろいです。今回は一万円札の肖像でおなじみ、福沢諭吉が設立した慶應義塾の中等部の入試問題に挑戦してみましょう。
問題
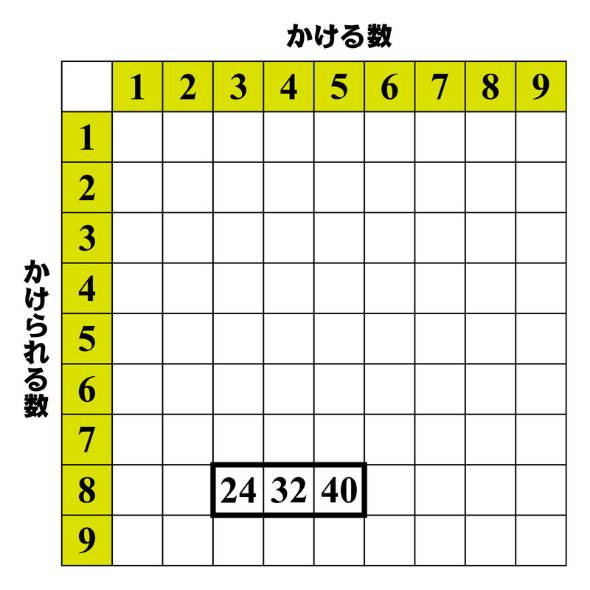
九九の答えが書かれた表で横に隣り合う3マスを枠で囲みます。
例えば図の場所に枠を作ると24と32と40を囲んだことになり、3つの数字を合計すると96です。
では、3つの数字の和が63になるような枠はいくつ作れるでしょう？
ただし、色のついている、かける数とかけられる数が書かれている部分は枠で囲みません。
＜平成29年度慶應義塾中等部入試問題・改題＞
九九の表での枠の置き方はたくさんあるので、一つ一つ計算して63になるかどうかを探すのは大変です。小学生でも一瞬にして解くことができるような素晴らしい解き方があるので、うまく発想しましょう。
解説
例えば24,32,40で考えましょう。
24は32よりも8小さい数で、40は32よりも8大きい数です。両端の数字と32との差はどちらも8なので、3つの平均値は32ですし、3つの和は32のちょうど3倍になります。
このように3つの数字を囲むと、「左の数が真ん中より小さいのと同じだけ、右の数は真ん中より大きい」ことが分かります。
よって、3つの数字の和は、必ず真ん中の数字の3倍になるのです。
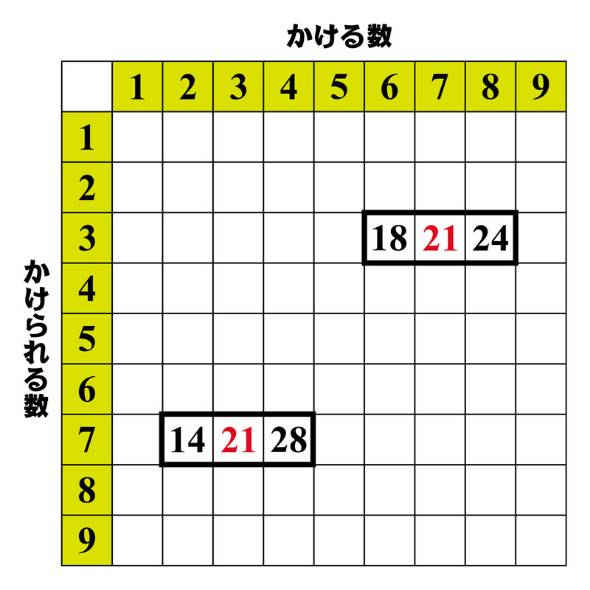
では、和が63になる枠の数を数えましょう。63は21の3倍なので、21が真ん中にくる枠を作ると和が63になるはずです。九九で答えが21になるのは3×7と7×3の2つだけです。
よって答えは2つです。
実は、思い付いたらほんの数秒で解ける問題でした。これは改題したもので、実際に出題された問題は最後の計算がもっと複雑ですが、やはり最大のポイントは真ん中の3倍であるということに気付けるかどうかです。観測できる事実から法則を見いだすことができるかどうかが合否を分けます。
他にもある！ 名門中学の入試問題
関連記事
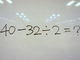「40−32÷2＝？」この問題、解けますか？
理系にはすぐ解けて、文系には解けない、とんち問答のような問題がネットで話題に。
「日本一賢い小学生」はこんな問題を解いている！ 名門・灘中学の入試、解けますか？
あなたは日本一賢い小学生に勝てますか？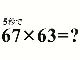
「67×63」を一瞬で解けるようになる方法
インド人に学ぶヴェーダ数学。
これ12歳が解けるの!? 超難関「灘中学」の入試問題「初日の出を2回見るには？」を解いてみた
あなたは最強小学生に勝てるか？
「訃報」「愛猫」「手風琴」って読める？ 常用漢字表に掲載されている“難読漢字”
ニュースなどでよく見る表現も、意外と分からん……。
Copyright © ITmedia, Inc. All Rights Reserved.
パパに抱っこされている娘→11年後…… 同じ場所＆ポーズで撮影した“現在の姿”が「泣ける」「すてき」と反響
「何があった」 絵師が“大学4年間の成長過程”公開→たどり着いた“まさかの境地”に「ぶっ飛ばしてて草」
「ほ、本人……？」 日本に“寒い国”から飛行機到着→降りてきた“超人気者”に「そんなことあるw？」「衝撃の移動手段」の声
才賀紀左衛門、娘とのディズニーシー訪問に“見知らぬ女性の影” 同伴シーンに「家族を大切にしてくれない人とは仲良くできない」
【今日の難読漢字】「誰何」←何と読む？
「今やらないと春に大後悔します」 凶悪な雑草“チガヤ”の大繁殖を阻止する、知らないと困る対策法に注目が集まる
武豊騎手が2024年に「武豊駅に来た」→実は35年前「歴史に残る」“意外な繋がり”が…… 街を訪問し懐古
大谷翔平、“有名日本人シェフ”とのショット 上目遣いの愛犬デコピンも…… 「びっくりした!!」「嬉しすぎる」
ハローマックのガチャに挑戦！ →“とんでもない偏り”に同情の声 「かわいそう」「人の心とかないんか」
古着屋で“インパクト大”なブランケットをリメイクすると…… 劇的な仕上がりに386万再生「これはいいね、欲しい！」【海外】
- パパに抱っこされている娘→11年後…… 同じ場所＆ポーズで撮影した“現在の姿”が「泣ける」「すてき」と反響
- 「何があった」 絵師が“大学4年間の成長過程”公開→たどり着いた“まさかの境地”に「ぶっ飛ばしてて草」
- 「中学生で妊娠」した“14歳の母”、「相手は逃げ腰」妊娠発覚からの経緯を赤裸々告白 母親の“意外な反応”も明かす
- 勇者一行が壊滅、1人残った僧侶の選択は……？ 「ドラクエでのピンチ」描くイラストに共感「生還できると脳汁」
- 「笑い止まらん」 海外産アプリで表示された“まさかの日本語”に不意打ち受ける人続出 「何があったんだw」
- パパが好きすぎる元保護子猫、畑仕事中もくっついて離れない姿が「可愛すぎる」と反響 2年以上がたった現在は……飼い主に話を聞いた
- アグネス・チャン、米国の自宅が“度を超えた面積”すぎた……ゴルフ場内に立地＆門から徒歩5分の豪邸にスタッフ困惑「入っていいのかな」
- 「理解できない」 大谷翔平と真美子さんの“スキンシップ”に海外驚き 「文化は100%違う」「伝説だわ」
- 「車が憎い」 “科捜研”出演俳優、交通事故で死去 兄が悲痛のコメント「忘れないでください」
- PCで「Windowsキー＋左右矢印キー」を押すと？ アッと驚く隠れた便利機能に「スゲー便利」「知らなかった」
- 「何言ったんだ」 大谷翔平が妻から受けた“まさかの仕打ち”に「世界中で真美子さんだけ」「可愛すぎて草」
- 「絶句」 ユニクロ新作バッグに“色移り”の報告続出…… 運営が謝罪、即販売停止に 「とてもショック」
- 「飼いきれなくなったからタダで持ってきなよ」と言われ飼育放棄された超大型犬を保護→ 1年後の今は…… 飼い主に聞いた
- アレン様、バラエティー番組「相席食堂」制作サイドからのメールに苦言 「偉そうな口調で外して等と連絡してきて、」「二度とオファーしてこないで下さぃませ」
- 「明らかに……」 大谷翔平の妻・真美子さんの“手腕”を米メディアが称賛 「大谷は野球に専念すべき」
- 「やはり……」 MVP受賞の大谷翔平、会見中の“仕草”に心配の声も 「真美子さんの視線」「動かしてない」
- ドクダミを手で抜かず、ハサミで切ると…… 目からウロコの検証結果が435万再生「凄い事が起こった」「逆効果だったとは」
- 「母はパリコレモデルで妹は……」 “日本一のイケメン高校生”グランプリ獲得者の「家族がすごすぎる」と驚がくの声
- 「ごめん母さん。塩20キロ届く」LINEで謝罪 → お母さんからの返信が「最高」「まじで好きw」と話題に
- 「真美子さんさすが」 大谷翔平夫妻がバスケ挑戦→元選手妻の“華麗な腕前”が話題 「尊すぎて鼻血」