この図形の面積、三平方の定理を使わずに出せる？ ヒラメキで解く“算数”がちょっと手ごわい
こういう問題をスッと解ける子どもでありたかった……。
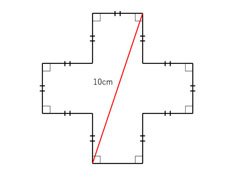
十字型の図形の面積を問う小学生向けの問題が、「これは良問」と好評です。「算数」の知識だけで解けるかな？
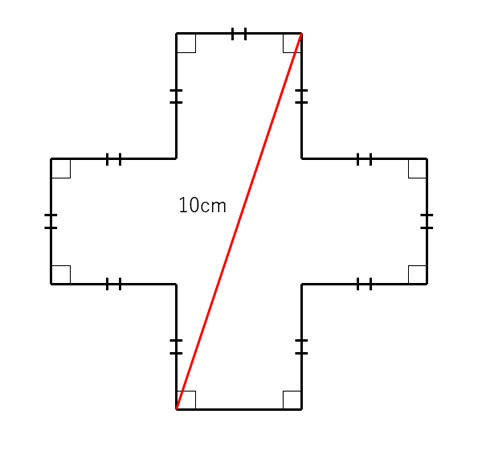
Twitterユーザーのロボ太（@kaityo256）さんが、「息子の塾で出たのがちょっと面白かった」と紹介した問題。出題の図形は同寸の正方形を5つ並べたような十字型で、寸法に関する情報は、対角に入った赤線の長さが10センチであることだけです。大人としては、これを手がかりに三平方の定理を用いて1辺の長さを求めたくなるところですが、これはあくまでも算数の問題。がまんして別の工夫で解くのが筋というものでしょう。
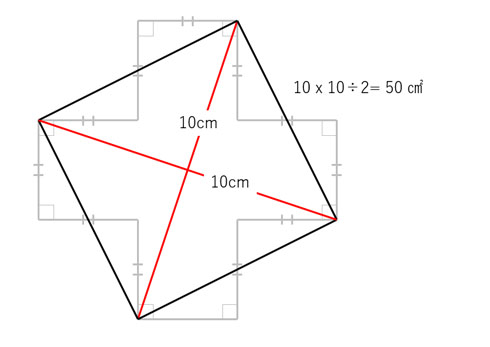
解法は2つあり、1つは図形を赤線で切って2等分したものを、4つ分並べて1辺10センチの正方形を作る方法。その面積を求めて半分にすればもともとの面積が割り出せるわけで、答えは10×10÷2で50平方センチメートル。
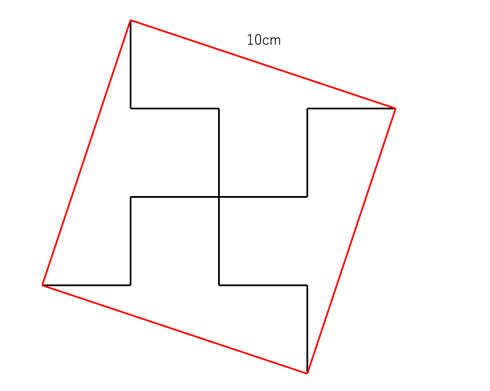
もう1つは、赤線に対して同じ長さの補助線を直交するように引く方法。さらに線の端を補助線で結ぶと、元の図形が赤線を対角線とする正方形へ組み替えられた格好が見えてきます。正方形の面積は「対角線の長さ×対角線の長さ÷2」でも求められるので、答えはやはり10×10÷2で50平方センチメートル。
ツイートには「算数の領分で解く小学生向けの問題と考えると、逆に難しい」「大人は『1辺がルート10センチの正方形が5個並んでいる』と知覚するのですが、子どもは見え方が違うのですね」など、考え込む大人の反応が多数。ロボ太さんは「小学生向けの問題には、進んだ知識があるとかえって解けなくなるものがありますよね……」と述べています。
画像提供：ロボ太（@kaityo256）さん
関連記事
「16×4は？」「68−4だから64」 小学1年生の掛け算の計算方法が斬新だと話題に
発想が見事。
「40÷5は？」「5＋5が10で4＋4が8だから答えは8」割り算を巡る親子の会話 小1の息子はどう解いた？
息子さん天才でしょ。
【数式で見ると分かる】“蛇口から出る水、下に行くほど細くなる現象”の理由
水が減っているわけではないのに、なぜ細くなる？
「三平方の定理」がひと目で分かる展示が面白いと話題に 「視覚的にわかる」「こういうのが学校にあったら」
液体の動きで見るとよりワクワクできます。
算数が苦手な娘のため父親が計算問題でゾンビと戦う学習ゲームを開発→娘さん大喜び、正式リリースへ
「算数 オブ ザ デッド」と、Twitterでも大好評。
「ガムは75円。ガムはクッキーより40円安いそうです。チョコは何円？」 小2向けドリルの難問が誰にも解けない
出題ミスのせいで、ダウンタウンの「太郎くんが花を買いに行きました。さて、どうでしょう」レベルの難易度に。
「算数が苦手な小学生時代、自力で考えた“先生には理解できない解き方”の方が早くて使えた」というお話
速さの公式を覚えることも大事だけど「本質を考えたりすれば導き出せるかも」。
関連リンク
Copyright © ITmedia, Inc. All Rights Reserved.
猫だと思って保護→2年後…… すっかり“別の生き物”に成長した元ボス猫に「フォルムが本当に可愛い」「抱きしめたい」
「やはり……」 MVP受賞の大谷翔平、会見中の“仕草”に心配の声も 「真美子さんの視線」「動かしてない」
大きくなったらかっこいいシェパードになると思っていたら…… 予想を上回るビフォーアフターに大反響！→さらに1年半後の今は？ 飼い主に聞いた
「大企業の本気を見た」 明治のアイスにSNSで“改善点”指摘→8カ月後まさかの展開に “神対応”の理由を聞いた
「明らかに……」 大谷翔平の妻・真美子さんの“手腕”を米メディアが称賛 「大谷は野球に専念すべき」
「何言ったんだ」 大谷翔平が妻から受けた“まさかの仕打ち”に「世界中で真美子さんだけ」「可愛すぎて草」
松田翔太、憧れ続けた“希少な英国製スポーツカー”をついに入手「14歳の僕に見せてあげたい」 過去にはフェラーリやマクラーレンも
「行きたすぎる」 入場無料の博物館、“宝石展を超えた宝石展”だと40万表示の反響 「寝れなくなっちゃった」【英】
スーパーで売っていた半額のひん死カニを水槽に入れて半年後…… 愛情を感じる結末に「不覚にも泣いてしまいました」
自動応答だと思って公式LINEに長文を送ったら…… 恥ずかしすぎる内容と公式からの手動返信に爆笑 その後について聞いてみた
- 「飼いきれなくなったからタダで持ってきなよ」と言われ飼育放棄された超大型犬を保護→ 1年後の今は…… 飼い主に聞いた
- ドクダミを手で抜かず、ハサミで切ると…… 目からウロコの検証結果が435万再生「凄い事が起こった」「逆効果だったとは」
- 「明らかに……」 大谷翔平の妻・真美子さんの“手腕”を米メディアが称賛 「大谷は野球に専念すべき」
- まるで星空……!! ダイソーの糸を組み合わせ、ひたすら編む→完成したウットリするほど美しい模様に「キュンキュンきます」「夜雪にも見える」
- 妻が“13歳下＆身長137センチ”で「警察から職質」 年齢差＆身長差がすごい夫婦、苦悩を明かす
- 人生初の彼女は58歳で「両親より年上」 “33歳差カップル”が強烈なインパクトで話題 “古風を極めた”新居も公開
- 「ごめん母さん。塩20キロ届く」LINEで謝罪 → お母さんからの返信が「最高」「まじで好きw」と話題に
- 互いの「素顔を知ったのは交際1ケ月後」 “聖飢魔IIの熱狂的ファン夫婦”の妻の悩み→「総額396万円分の……」
- ユニクロが教える“これからの季節に持っておきたい”1枚に「これ、３枚色違いで買いました！」「今年も色違い買い足します！」と反響
- 中央道から「宇宙戦艦ヤマト」が見える！ 驚きの写真がSNSで注目集める 「結構でかい」「どう見てもヤマト」 撮影者の心境を聞いた
- 50年前に撮った祖母の写真を、孫の写真と並べてみたら…… 面影が重なる美ぼうが「やばい」と640万再生 大バズリした投稿者に話を聞いた
- 「食中毒出すつもりか」 人気ラーメン店の代表が“スシローコラボ”に激怒 “チャーシュー生焼け疑惑”で苦言 運営元に話を聞いた
- フォロワー20万人超の32歳インフルエンサー、逝去数日前に配信番組“急きょ終了” 共演者は「今何も話せないという状態」「苦しい」
- 「顔が違う??」 伊藤英明、見た目が激変した近影に「どうした眉毛」「誰かとおもた…眉毛って大事」とネット仰天
- 「ごめん母さん。塩20キロ届く」LINEで謝罪 → お母さんからの返信が「最高」「まじで好きw」と話題に
- 星型に切った冷えピタを水に漬けたら…… 思ったのと違う“なにこれな物体”に「最初っから最後まで思い通りにならない満足感」「全部グダグダ」
- 「泣いても泣いても涙が」 北斗晶、“家族の死”を報告 「別れの日がこんなに急に来るなんて」
- ジャングルと化した廃墟を、14日間ひたすら草刈りした結果…… 現した“本当の姿”に「すごすぎてビックリ」「素晴らしい」
- 母親は俳優で「朝ドラのヒロイン」 “24歳の息子”がアイドルとして活躍中 「強い遺伝子を受け継いだ……」と注目集める
- 「幻の個体」と言われ、1匹1万円で購入した観賞魚が半年後…… 笑っちゃうほどの変化に反響→現在どうなったか飼い主に聞いた