どうぶつタワーバトルで勝つ方法、物理学的に教えます キーワードは「トルクをゼロにせよ」

レートを上げて、物理（学）で積めばいい。

[QuizKnock，ねとらぼ]

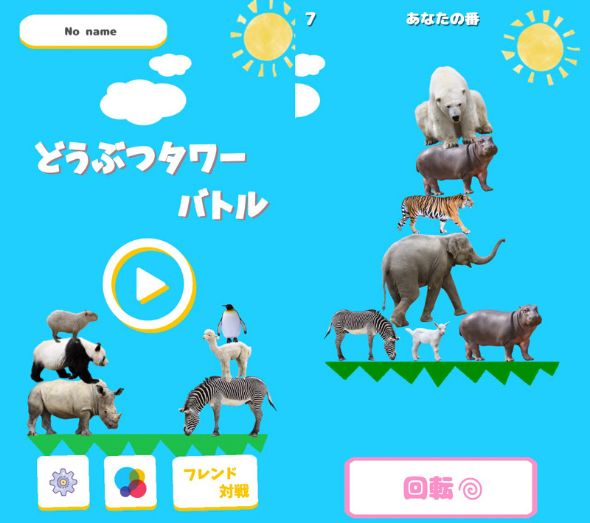
　ゲーム事情に詳しい皆さんならもうご存じとは思いますが、筆者もハマっております、どうぶつタワーバトル。

　「2人で交互に動物を積んでいき、ステージから落下させたら負け」というシンプルなルールながら、動物たちの複雑な形状から思いもよらないバランスが生まれて大笑いしたり、勝敗に応じて上下する対戦レートでアツくなったりと楽しめる作品です。

　12月が始まってすぐのアプリランキングで1位を獲得しており、2017年を代表するスマホゲームの1つといっても過言ではないでしょう。ブームが1カ月早かったら、ユーキャンの新語流行語大賞に選ばれていたかもしれません。

　……ちなみに「やべ、知らない！」という人も今すぐ始めれば、明日には友達と話せるようになるはず。取っ付きやすさもどうぶつタワーバトルの魅力です。

筆者の対戦プレイ動画。通算500戦くらいやっています

　さて、このゲームの肝となるのは「動物をバランス良く積むこと」。しかし、どうすれば、この“良いバランス”が見極められるようになるのでしょうか。

　物理学的に答えると、「力のモーメント」や「トルク」と呼ばれる量がキーワードになります。

どうぶつタワーバトルの合言葉は「トルクをゼロにせよ」

　トルクとは、物を回転させる力のことです。物理学では、物を動かすときに加える力を「力（Force）」、物を回転させて向きを変えるときに加える力を「トルク（Torque）」と呼びます。

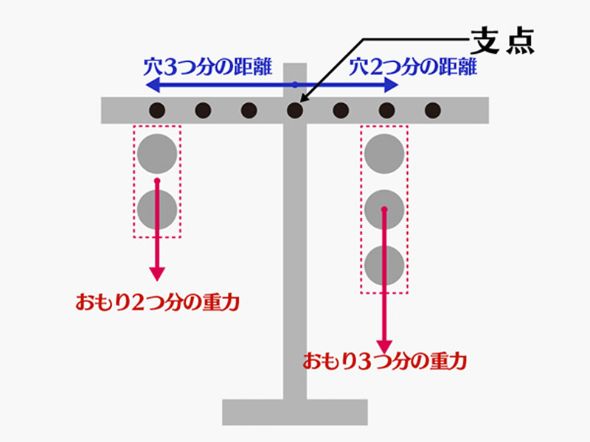
　思い出してほしいのは、小学校でのてんびんの実験です。重さが同じおもりでも、てんびんの腕のどこに引っ掛けるかで右に傾いたり左に傾いたりしましたよね。同じ重力（力）でも、回転させるはたらき（トルク）はおもりを置く場所によって変わってしまうのです。

　トルクは「支点からの距離（回したい方向に対して垂直に測る）×力」で計算されます。距離が長ければ長いほど、力が大きければ大きいほど、回す力（トルク）は大きくなります。

おもりの数が違っても釣り合うのは、支点との距離がトルクの大小に関わるため

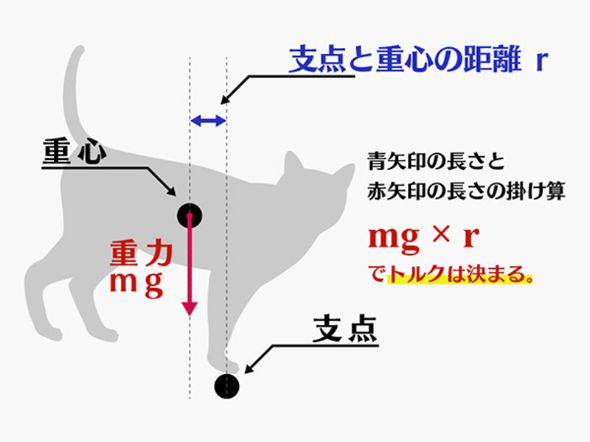
　どうぶつタワーバトルではたらいている力は、重力だけです。重力とは「重心に全ての重さが集まったと考え、それが真下に引っ張られる力」なので、重力は重心にのみかかっていると見なして構いません。そこで、どうぶつタワーバトルに即したトルクの計算式は、次のようになります。

　「動物が回る力（トルク）＝動物の重さ（重力）×動物の重心から支点までの距離」

　この「動物が回る力（トルク）」がゼロになれば、動物は回転しません。つまり、積む動物の重心が、地面や他の動物と接する点の真上にくると（重心と支点の距離をゼロにすると）、倒れたり転がったりしないというわけです。

　例えば、向きを変えていない状態のトナカイ（通称「0トナカイ」）は重心が前足の真上にあり、支点との距離がゼロ。このため、前足一本だけで立つことができます。

大きな角があるトナカイの重心は前足の真上

　シロクマの必殺技と名高い「ラムセウム・テンティリス」（シロクマの上に逆さにしたシロクマを重ねて置く技）も、シロクマの重心が体の真ん中、頭の真下にあるからこそ成立する技です。

めちゃくちゃ不安定に見えますが、上のシロクマは落下しません

物理学で分かる「守りの2キリン」の強さ

　もう1つ大事なことは「支える点が3つあり、その3点の間に重心があれば、必ずトルクをゼロにできる」ということです。身近なところでいうと、カメラの三脚が安定して立つのは、この法則を利用しているためです。

　ですが、どうぶつタワーバトルは2次元の世界なので、支える点は2つで十分。つまり、支点となる2点の間に重心を置くようにすればいいのです。

　これを理解すれば、2度「回転」ボタンを押し、90度回したトラ（通称「2トラ」）や「6カバ」が倒れずに直立する理由が分かるようになります。

　また、どうぶつタワーバトル界の格言「守りの2キリン」の由来も納得できるようになるはず。この構えのキリンは顔と脚が大きく左右に離れており、重心のある胴体は必ずこの2点の間に来ます。だから、守りに適した高い安定性を発揮できるのです。

後ろ足からお尻にかけてのラインに次の動物を置きやすい点も、「守りの2キリン」の強さ

• 1点で支えるなら、その真上に重心
• 2点で支えるなら、その間に重心

　これを心掛ければ、どうぶつタワーバトルで高レートが目指せるはず。ちなみに、筆者は崖つかみの練習をしまくったせいで、レートが1300まで落ちてしまいましたが……。

制作協力

QuizKnock