【指数関数的な増え方】数学の基本から理解する“新型コロナで外出自粛などが求められる理由”（2/2 ページ）

[キグロ，ねとらぼ]

「国別の感染者数」などに使われる対数グラフとは

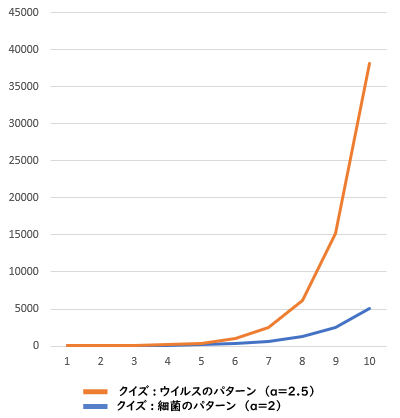
　前段でも掲載しましたが、細菌のパターン（2倍、そのまた2倍、そのまた2倍……と増えていく）、ウイルスのパターン（2.5倍に増えていく）をグラフ化してみると、後者の方が圧倒的に増えることがはっきりと分かります。

　……ただ、こういうグラフの描き方には、欠点があります。縦軸の値があまりにも大きいため、細かい部分がどうなっているのか、よく分からないのです。

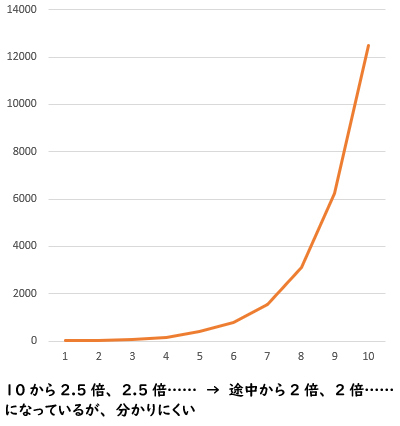
　また、途中から増加の仕方が変わっていたとしても、グラフからはよく分かりません（下記のグラフでは、途中から2.5倍→2倍に変わっている）。新型コロナウイルスを例に取ると、これは「感染防止のために、外出自粛などを呼び掛ける→それによって感染の広まりを押さえられたか（実行再生産数が変わったか）が、グラフからうまく読み取れない」ということです。

　こういうときに使われるのが「対数グラフ」。ニュースで見掛ける「国別の感染者数」などにも使われています。

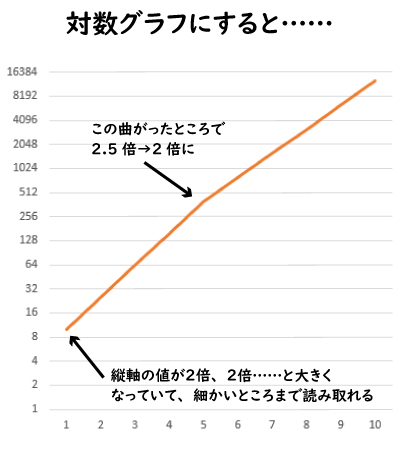
　下記の対数グラフは「10から2倍、そのまた2倍、そのまた2倍……と増えていく」場合のもの。縦軸の目盛りも同様に2倍2倍に並んでおり、2、4、8、16、32、64……と増加。このようにすると指数関数的増大のグラフは直線で描くことができ、もしも増え方が変われば（新型コロナウイルスの感染者数でいうと、実効再生産数が変われば）、そこで折れ曲がるので変化が一目で分かります。

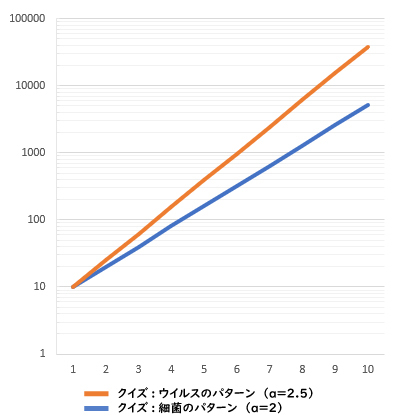
　対数グラフの縦軸に2をかけた数を書きましたが、10をかけた数にしても構いません。それで細菌のパターン、ウイルスのパターンをグラフ化してみるとこうなります。

　なんだか変わった縦軸になりましたね。縦に一、十、百、千、万……と並んでいますが、その間にうっすらと描いてあるいてある1〜9、10〜90、100〜900……の線は等間隔になっていません。対数グラフの仕様ですね。

　もしも新型コロナウイルス関連のニュースでグラフが出てきたら、縦軸に注目してみてください。